Chapter 7: Mathematics in Grades Three Through Five

Figure 7.1. A Progression Chart of Big Ideas, Grades Three Through Five (Figure 6.16 in the 2023 CA Mathematics Framework)

Content Connections	Big Ideas: Grade Three	Big Ideas: Grade Four	Big Ideas: Grade Five
Reasoning with Data	Represent Multivariable data	Measuring and plotting	Plotting patterns
Reasoning with Data	Fractions of shape and time	Rectangle Investigations	Telling a data story
Reasoning with Data	Measuring	n/a	n/a
Exploring Changing Quantities	Addition and subtraction patterns	Number and shape patterns	Telling a data story
Exploring Changing Quantities	Number flexibility to 100	Factors and area models	Factors and groups
Exploring Changing Quantities	n/a	Multi-digit numbers	Modeling
Exploring Changing Quantities	n/a	n/a	Fraction connections
Exploring Changing Quantities	n/a	n/a	Shapes on a plane
Taking Wholes Apart, Putting Parts Together	Square tiles	Fraction flexibility	Fraction connections
Taking Wholes Apart, Putting Parts Together	Fractions as relationships	Visual fraction models	Seeing Division
Taking Wholes Apart, Putting Parts Together	Unit fraction models	Circles, fractions and decimals	Powers and place value
Discovering Shape and Space	Unit fraction models	Circles, fractions and decimals	Telling a data story
Discovering Shape and Space	Analyze quadrilaterals	Shapes and symmetries	Layers of cubes
Discovering Shape and Space	n/a	Connected problem solving	Shapes on a plane

The upper-elementary grades present new opportunities for developing and extending number sense. There are four Big Ideas related to number sense for grades three through five including:

• extending flexibility with numbers;
• understanding the operations of multiplication and division;
• making sense of operations with fractions and decimals; and
• using number lines as tools.

As students learn to think about numbers flexibly, by composing and decomposing numbers, they will learn to recognize the inverse relationship between addition and subtraction and between multiplication and division. If students are given meaningful explorations with numbers and number patterns, they will develop memories of mathematics facts, and the memories will be meaningful and conceptual. As students learn in these grades to identify and express patterns, both visually and numerically, they will build foundations for proportional reasoning when thinking about the connections between units. In fifth grade, the flexibility students have developed with numbers can be applied to fractions and to the place value system.

Students in the upper-elementary grades learn to conduct data investigations, which include asking and answering questions that are of interest to them. They learn to collect and analyze data, determine, and confirm results, and communicate their findings. While the data visualizations set out in the standards in these grades only include picture graphs, bar graphs, and line plots, students do not need to be restricted to these.

Students investigate patterns and relationships in 2-D and 3-D space, and they begin to use the coordinate plane to represent and question relationships. As students learn about 3-D space, they build understanding of the volume as a quantity of unit cubes that fill the space of a solid. Students study time as a measure and connect the central angles of a circle to the clock face and hands. The study of the clock face is another area for connections between numbers and fractions, as students learn about and communicate detailed measures of time.

Students who are ELs are encouraged to use their developing English and native language assets and draw on their prior knowledge. Teachers can examine text and tasks for key language forms and structures, and general as well as discipline-specific, high-utility academic vocabulary words linked to the Big Ideas and connections. Teachers can provide purposefully planned and “just-in-time” scaffolds and supports to engage EL students in sustained mathematical discourse in multiple contexts to build academic language and knowledge.

The following vignette highlights an educator who is using digital tools to allow students to better visualize concepts introduced at this grade span.

---

Vignette
Polygon Properties Puzzles

Students in Ms. Thompson’s fourth-grade class have been exploring the attributes of polygons. They have compared and contrasted physical models and illustrations of polygons, attending to features such as angle size, number of sides, and whether the figures have any parallel or perpendicular sides. Lessons have included polygons that students view as “typical” as well as atypical examples. Today, Ms. Thompson will ask her students to draw polygons that meet specific criteria as a way to show their understanding. Her planning is informed by an adaptation of five challenges from About Teaching Mathematics (Burns, 2007). Students will illustrate the figures using technology, specifically Whiteboard. Some of the standards addressed in the lesson include:

• SMP.1, 3, 5, 6, 7
• Content Standards: 3.G.1; 4.G.1, 2, 4.MD.5; 5.G.3, 4
• ELD Standards: PI.1; PI.2; PI.3; PI.4; PI.5; PI.9; PI.12

Ms. Thompson is deliberate and selective in the use of technology. She plans to use Whiteboard for this lesson as she finds it can facilitate the use of mathematical practices and increase focus on the mathematics content. Her expectation is that this use of technology will

• reduce the challenge of drawing straight lines by using Whiteboard’s line tool;
• encourage collaboration and discourse between partners who are sharing one Chromebook, and later, among the larger group;
• support linguistically and culturally diverse ELs;
• support students with learning differences in accessing the tasks and finding meaning in their learning;
• increase engagement for the many students who are enthusiastic users of technology;
• foster growth mindsets and promote the correction of errors and revision of work in progress;
• enable the class to see and compare various student products in a highly visible, large-scale format via Google Casting or the link sharing within Whiteboard;
• use class time efficiently, allowing for full discussion and analysis; and
• serve as a quick way to engage in the formative assessment process as student work is instantly transmitted to the teacher’s view.

Ms. Thompson uses Google Classroom (and is familiar with other learning management systems) and Whiteboard (by the Math Learning Institute) often for lessons. These students have worked in collaborative groups for several months, sharing and explaining their thinking digitally. They share their work using links or the share code and posting them into their assignments on Google Classroom. The class has established effective collaboration protocols (e.g., stay on your own page, let everyone speak, do not delete others’ work, add to someone else’s thinking, everyone has equal access to the tool). Students are arranged in four-person table groups. They know how to partner up and then switch partners in their table group quickly. The class has a system for Chromebook management: One partner is responsible for getting two Chromebooks out before the morning meeting; the second partner returns the devices to the charging station during afternoon cleanup time.

The teacher considered language barriers and the needs of individual students as she planned partners and heterogeneous groups. Ms. Thompson has 12 ELs in this class. To support their learning, she

• has placed the one Emerging EL student with a language-proficient Spanish-speaking student to help with translations and collaboration;
• will create and display sentence frames for this student to use during discussion and collaboration;
• provided the seven ELs who are at the Bridging stage and the four ELs who are at the Expanding level with sentence stems to support them as they discuss and explain their thinking;
• has paired a student with an IEP for reading with a student who can help them access the written material; and
• situated two students who have IEPs for math with partners who are supportive and able to share the work equitably and inclusively.

In this lesson, students will use a familiar classroom routine, “Convince Yourself, a Friend, a Skeptic.” They will

1. solve each problem with a partner (convince yourself);
2. justify their mathematical argument to the other pair in their table group, who will ask questions and encourage further explanation (convince a friend); and
3. prepare to convince the class, who will challenge and probe any inconsistencies (convince a skeptic).

Ms. Thompson begins the lesson by focusing attention on an image the class explored the day before: a square that is not oriented on the horizontal. She asks partners to describe the figure using precise mathematical terms, as they did in the previous lesson.

Students offer many of the terms that emerged in the earlier lesson, which Ms. Thompson records for the class: square, rectangle, tilted square, diamond, right angles, square corners, parallel sides, perpendicular, equal side lengths. Several students raise their hands to challenge the term “diamond,” arguing that it is an informal term and that “a square is still a square, even if it is tilted!” Ms. Thompson comments that students have shown they could convince others and could take the role of skeptics; she encourages them to continue to attend to the properties of polygons in today’s lesson, too.

Ms. Thompson tells the students that this time, they will share one Chromebook with their designated partner, using Whiteboard to illustrate a series of polygons with particular properties. This causes excitement among her students; almost all are enthusiastic about using Whiteboard and working with their partners.

Ms. Thompson tells the class that they will draw a series of polygons that include specific properties. As she posts each one, students will read the task aloud together and then think quietly about how they might draw the figure. Once they have an idea, they should show a “thumbs up” to signal that they are ready to start work on the Chromebook. After partners solve each problem, they must convince the other partners at the table and plan to explain and justify their thinking in the whole-class “skeptics” discussion.

Ms. Thompson posts Task 1: “Make a triangle with one right angle and no two sides the same length.”

The class reads the statement aloud twice, carefully and slowly. Ms. Thompson signals for quiet thinking and watches as students begin responding with their thumbs up. When she is satisfied that partners are ready to begin, she invites them to start illustrating on Whiteboard.

As anticipated, students are successful and confident on the first task, having practiced by exploring triangles of various types. Ms. Thompson displays four student responses for the class to consider, selecting examples that are oriented differently. Some students express surprise about how many different ways the figure can be drawn and still meet the requirements. Ms. Thompson asks students to talk with their partners, using the sentence frames as necessary in their role as skeptics, and be ready to question, challenge, or probe any inconsistencies they note in the triangles displayed. After a few moments, a few questions/challenges are posed:

• How can we tell if C has a right angle when it’s “lying down” like that?
• Is B really a right-angle triangle if the right angle is pointing to the left?
• Convince us about D, too! It’s pointing to the left!

Ms. Thompson invites the partners whose images are being questioned to respond. In two cases, students ask if they can measure side lengths to assure that they are all different. Ms. Thompson allows the class to reach consensus independently, agreeing that all four examples are right triangles with three sides of different lengths.

Ms. Thompson presents Task 2: “Make a triangle with exactly two congruent angles.”

The procedures from the first task are duplicated here: read aloud, pause to think, then collaborate with a partner—but this time the second partner is the lead illustrator.

Ms. Thompson circulates, stopping beside her Emerging English learner student and partner to listen. To provide support for but not single out her Emerging English learner student, she asks the pair to draw or use hands to demonstrate what is meant by “congruent” angles. A brief exchange assures her that the partners are working effectively; she reminds the pair to rehearse how they could defend their illustration to their table partners and the class. Several student pairs are discussing congruence as she moves through the groups, some referring to their journals or the word wall listing mathematics terms. In quick check-ins with the remaining groups comprised of English learner students, Ms. Thompson notes that two of the Bridging students are letting their partners do most of the talking; she reminds students of the classroom norms related to “equal voices,” then engages with each pair in ways that engage the quieter students. After instilling this balance, she encourages each, noting that partner time is a time for safe practice. Before leaving each group, she reminds the students that what she has heard is worth sharing when the time comes to discuss with the class, inviting her English learner students to reiterate for their peers what they developed in pairs.

When Ms. Thompson posts several students’ illustrations, she includes an example with three congruent angles, not “exactly” two as the task specified. This non-example promotes energetic discussion and respectful challenges from friendly skeptics.

The class continues with two more tasks:

Task 3: “Make a four-sided polygon with no parallel sides.”

Task 4: “Make a four-sided polygon with one right angle and all sides different lengths.”

As Ms. Thompson circulates, encourages, and listens intently, she acquires insights into students’ understandings and strengths, and uncovers a few misconceptions. She notes with satisfaction that students are actively using mathematical practices, in particular, SMPs 3 and 6. These observations guide her as she orchestrates the skeptics’ discussion for each task.

Ms. Thompson will use students’ responses to the final task, an exit ticket, as a formative assessment. She has designed two exit tickets so that each student can express and share their own understanding independently rather than with support from their partner.

She tells the class that rather than repeating the “Convince Yourself, a Friend, a Skeptic” routine, they will respond independently. Each student may choose to respond using paper and pencil or Whiteboard. Those who respond digitally share their work via the link sharing button and post it into their Google Classroom assignment. The paper copies are collected.

The exit ticket tasks involve concepts of parallel sides and angle measurement, which are key understandings in the grade four standards (4.MD.5, 6; 4.G.1,2).

Task 5:

A. Make a four-sided polygon with no right angles but with opposite sides parallel.

B. Make a four-sided polygon with at least two angles greater than 90 degrees.

As she reflects on the lesson, Ms. Thompson notes the following:

• Whiteboard’s immediacy expedited the students’ creation, and the teacher’s selection and presentation, of work samples.
• Images were large, detailed, and easily viewed by all students.
• With few exceptions, students were engaged throughout the lesson.
• All students were able to use the technology to make their own polygons.
• Partners shared the use of the device smoothly.
• The level of challenge was appropriate for almost all students.
• Three of the seven EL students who are at the Bridging stage were willing to speak with their individual partners but remained quiet in table and whole-class discussions.
• Two of the four EL students at the Expanding level justified their reasoning confidently during the whole-class discussion.

During the next lesson, Ms. Thompson will create an opportunity for students to correct any misunderstandings that were revealed, as well as solidify their learning by sharing and analyzing examples of Task 5 illustrations.

---

Grade Three

In third grade, students extend their work from second grade, thinking with groups, to equal groups and rows and columns in multiplication. As students learn to think about numbers flexibly, by composing and decomposing numbers, they will learn to recognize the inverse relationship between multiplication and division. Being flexible with numbers is an important component of fluency, rather than a focus on being fast with computation. The Mathematics Framework defines fluency:

Fluency means that students use strategies that are flexible, efficient, and accurate to solve problems in mathematics. Students who are comfortable with numbers and who have learned to compose and decompose numbers strategically develop fluency along with conceptual understanding. … In the past, fluency has sometimes been equated with speed, which may account for the common but counterproductive use of timed tests for practicing facts (Henry & Brown, 2008).

Being flexible is a Big Idea and one which draws from connections between numbers and patterns. When students develop number sense, they have a flexible internal framework that they can draw upon when working with any mathematics. Note that while students in third grade do begin to divide numbers, they do so using strategies as distinguished from formal algorithms.

Third grade is also the time when fractional thinking begins to become robust and can begin with a deep understanding of one-half that students can build on to understand and visualize other unit fractions.

Students can be given plenty of time to “play” with numbers and fractions, to think about their relative size, and to estimate and reflect on whether their answers make sense (SMP.3, 7, 8). Students in third grade focus on understanding fractions as equal parts of a whole and as numbers located on the number line. They also use reasoning to compare unit fractions (3.NF.1, 2, 3).

In third grade, students can conduct data investigations and interpret data visuals through data talks. Contexts for questions to investigate should expand to include volume and mass measurement (grams, kilograms, and liters, but not compound units, such as cm³) in addition to the length, time, and money contexts from earlier grades (3.MD.A.2). Time measurements are refined to the nearest minute (3.MD.A.1), and length now includes half- and quarter-inches (3.MD.B.4). Beginning ideas of area give another possible context, limited here to areas that can be covered by a whole number of unit squares (3.MD.C.5, 3.MD.C.6).

Students continue refining their understanding of 2-D shapes, focusing on the similarities and differences between quadrilaterals. Students make sense of the attributes that make up these important shapes, that can all be composed by triangles. Students will recognize the importance of the triangle as the base unit, which connects with later learning of trigonometry and the method of dividing complex shapes into smaller triangles to find their area. Students investigate and quantify quadrilaterals and learn that area and perimeter are important measures, where perimeter is one-dimensional and area is 2-D. Having conversations about the base unit of measure helps students connect to the ideas of multiplication and division. Connecting numbers and shapes helps students to make other connections and build number sense.

Students who are ELs are encouraged to use their developing English and native language assets (e.g., cognates) and draw on their prior knowledge. Teachers can examine text and tasks for key language forms and structures, in addition to general and discipline-specific, high-utility academic vocabulary words linked to the Big Ideas and connections. Teachers can provide purposeful scaffolds and supports to engage EL students in sustained mathematical discourse in multiple contexts to build academic language and knowledge. Planned and “just-in-time” scaffolds and supports provide multiple entry points for meaning-making and sharing of ideas in mathematical ways and include representations, expression starters and builders, and targeted vocabulary and language structures (e.g., explanation, descriptions, comparisons, methods, and connections).

Critical Areas of Instructional Focus for Grade Three

Figure 7.2. Grade Three Big Ideas (Figure 6.52 in the 2023 CA Mathematics Framework)

Long description: The graphic illustrates the connections and relationships of some third-grade mathematics concepts.

Direct connections include:

• Fractions of Shape and Time directly connects to: Square Tiles, Fractions as Relationships, Unit Fractions Models, Represent Multivariable Data
• Measuring directly connects to: Number Flexibility to 100 in All Four Operations, Analyze Quadrilaterals, Represent Multivariable Data
• Patterns in Four Operations directly connects to: Number Flexibility to 100 in All Four Operations, Unit Fraction Models, Analyze Quadrilaterals, Represent Multivariable Data
• Square Tiles directly connects to: Fractions as Relationships, Number Flexibility to 100 in All Four Operations, Fractions of Shape and Time
• Fractions as Relationships directly connects to: Square Tiles, Fractions of Shape and Time, Unit Fraction Models
• Unit Fraction Models directly connects to: Fractions as Relationships, Patterns in Four Operations, Fractions of Shape and Time, Represent Multivariable Data
• Analyze Quadrilaterals directly connects to: Number Flexibility to 100 in All Four Operations, Patterns in Four Operations, Measuring
• Represent Multivariable Data directly connects to: Unit Fraction Models, Number Flexibility to 100 in All Four Operations, Patterns in Four Operations, Measuring, Fractions of Shape and Time
• Number Flexibility to 100 in All Four Operations, directly connects to: Square Tiles, Analyze Quadrilaterals, Represent Multivariable Data, Measuring, Patterns in Four Operations

Figure 7.2a. Grade Three Big Ideas, Content Connections, and Content Standards (Figure 6.53 in the 2023 CA Mathematics Framework)

Big Ideas	Content Connections	Grade Three Content Standards
Represent Multivariable Data	Reasoning with Data	MD.3, MD.4, MD.1, MD.2, NBT.1: Collect data and organize data sets, including measurement data; read and create bar graphs and pictographs to scale. Consider data sets that include three or more categories (multivariable data) for example, when I interact with my puppy, I either call her name, pet her, or give her a treat.
Fractions of Shape and Time	Reasoning with Data and Taking Wholes Apart, Putting Parts Together and Discovering Shape and Space	MD.1, NF.1, NF.2, NF.3, G.2: Collect data by time of day, show time using a data visualization. Think about fractions of time and of shape and space, expressing the base unit as a unit fraction of the whole.
Measuring	Reasoning with Data	MD.2, MD.4, NBT.1: Measure volume and mass, incorporating linear measures to draw and represent objects in 2-D space. Compare the measured objects, using line plots to display measurement data. Use rounding where appropriate.
Patterns in Four Operations	Exploring Changing Quantities	NBT.2, OA.8, OA.9, MD.1: Add and subtract within 1000––using student generated strategies and models, such as base 10 blocks, e.g., use expanded notation to illustrate place value and justify results. Investigate patterns in addition and multiplication tables, and use operations and color coding to generalize and justify findings.
Number Flexibility to 100 in All Four Operations	Exploring Changing Quantities	OA.1, OA.2, OA.3, OA.4, OA.5, OA.6, OA.7, OA.8, NBT.3, MD.7, NBT.1: Multiply and divide within 100 and justify answers using arrays and student generated visual representations. Encourage number sense and number flexibility––not “blind” memorization of number facts. Use estimation and rounding in calculation problems.
Square Tiles	Taking Wholes Apart, Putting Parts Together	MD.5, MD.6, MD.7, OA.7, NF.1: Use square tiles to measure the area of shapes, finding an area of n squared units, and learn that one square represents 1/nth of the total area.
Fractions as Relationships	Taking Wholes Apart, Putting Parts Together	NF.1, NF.3: Know that a fraction is a relationship between numerators and denominators––and it is important to consider the relationship in context. Understand why 1/2=2/4=3/6.
Unit Fraction Models	Taking Wholes Apart, Putting Parts Together and Discovering Shape and Space	NF.2, NF.3, MD.1: Compare unit fractions using different visual models including linear models (e.g., number lines, tape measures, time, and clocks) and area models (e.g., shape diagrams encourage student justification with visual models).
Analyze Quadrilaterals	Discovering Shape and Space	MD.8, G.1, G.2, NBT.1, OA.8: Describe, analyze, and compare quadrilaterals. Explore the ways that area and perimeter change as side lengths change, by modeling real world problems. Use rounding strategies to approximate lengths where appropriate.

Grade Four

Patterning and examining relationships are at the heart of fourth grade. Students begin to think about how to identify and express patterns, both visually and numerically, and build foundations for proportional reasoning when thinking about the connections between units. Students look within fractions and decimals for the relationships represented there—relationships between numerator and denominator, fraction and decimal, and decimal and place value. Fourth graders use relationships to connect multiplication and division and think flexibly across all operations.

After their introduction to multiplication in third grade, fourth-grade students employ that understanding to identify prime and composite numbers and to recognize that a whole number is a multiple of each of its factors. An excellent way for students to see the composition of numbers is the visual number activity. Students can also explore the multiplication table and highlight multiples with color or shape, looking for patterns and relationships.

At this grade, students develop an understanding of fraction equivalence by illustrating and explaining reasons for their conjectures and ideas. Students can strengthen their knowledge of fraction equivalence by engaging in games that provide practice, such as Matching Fractions or Fractional Wall, created by NRICH Maths¹. Students represent their thinking with diagrams (number lines, strip diagrams), pictures, and equations. This work lays the foundation for further operations with fractions in fifth grade.

Data investigations in fourth grade should include topics of student interest as students learn the ways to collect, analyze, and represent data. Line plots are introduced in fourth grade, and students can learn to create, read, and interpret different data displays, including line plots. When creating line plots, students can include fractional measurements to help bring fractions to life with real data, such as measurement of objects in the classroom or home.

In grade four, students move from seeing vertices as made up of an angle to more formal understandings of angles made of two rays with a common endpoint. The concept of a ray can lead to fascinating discussions of infinity that can captivate students. As students think about the addition of angles, they will again be connecting geometric ideas to number sense. The idea of a central angle of a circle, formed when two rays are joined at the center of a circle can connect with learning about the hands of a clock face. Students can investigate with angles in a myriad of ways. Students continue refining their work in measuring and quantifying the world around them by investigations, such as connecting the unit of measure from a square to a cube, as they use area, perimeter of shapes, and the volume of solids. These ideas connect to the operations of addition, subtraction, multiplication, and division. Students connect the unit of measure from a square to a cube as they use area and volume to make sense of space. These ideas can also be connected to fractions and decimals, building visual understandings and helping with the meaning of these operations.

Students who are ELs are encouraged to use their developing English and native language assets (e.g., cognates, morphological awareness) and draw on their prior knowledge. Teachers can examine text and tasks for key language forms and structures, and general as well as discipline-specific, high-utility academic vocabulary words linked to the Big Ideas and connections. Teachers can provide purposeful scaffolds and supports to engage EL students in sustained mathematical discourse in multiple contexts to build academic language and knowledge. Planned and “just-in-time” scaffolds and supports provide multiple entry points for meaning making and sharing of ideas in mathematical ways and include representations, expression starters and builders, and targeted academic vocabulary and language structures (e.g., problems, explanations, arguments, descriptions, procedures). Teachers guide deconstruction and/or co-construction of problems, investigations, arguments, explanations, descriptions, and procedures.

Critical Areas of Instructional Focus for Grade Four

Figure 7.3. Grade Four Big Ideas (Figure 6.54 in the 2023 CA Mathematics Framework)

Long description: The graphic illustrates the connections and relationships of some fourth-grade mathematics concepts.

Direct connections include:

• Number and Shape Patterns directly connects to: Shapes and Symmetries, Connected Problem Solving, Circles Fractions and Decimals, Factors and Area Models, Fraction Flexibility, Multi-Digit Numbers
• Shapes and Symmetries directly connects to: Connected Problem Solving, Circles Fractions and Decimals, Multi-Digit Numbers, Number and Shape Patterns
• Rectangle Investigations directly connects to: Connected Problem Solving, Measuring and Plotting, Circles Fractions and Decimals
• Connected Problem Solving directly connects to: Rectangle Investigations, Shapes and Symmetries, Number and Shapes Patterns, Multi-Digit Numbers, Circles Fractions and Decimals, Factors and Area Models, Measuring and Plotting
• Measuring and Plotting directly connects to: Connected Problem Solving, Rectangle Investigations, Visual Fraction Models
• Visual Fraction Models directly connects to: Measuring and Plotting, Circles Fractions and Decimals, Fraction Flexibility
• Factors and Area Models directly connects to: Connected Problem Solving, Circles Fractions and Decimals, Number and Shape Patterns, Multi-Digit Numbers, Fraction Flexibility
• Fraction Flexibility directly connects to: Factors and Area Models, Circles Fractions and Decimals, Number and Shape Patterns, Multi-Digit Numbers
• Multi-Digit Numbers directly connects to: Number and Shape Patterns, Shapes and Symmetries, Connected Problem Solving, Circles Fractions and Decimals, Factors and Area Models, Fraction Flexibility
• Circles Fractions and Decimals directly connects to: Multi-Digit Numbers, Number and Shape Patterns, Shapes and Symmetries, Rectangle Investigations, Connected Problem Solving, Visual Fraction Models, Factors and Area Models, Fraction Flexibility

Figure 7.3a. Grade Four Big Ideas, Content Connections, and Content Standards (Figure 6.55 in the 2023 CA Mathematics Framework)

Big Ideas	Content Connections	Grade Four Content Standards
Measuring and Plotting	Reasoning with Data	MD.1, MD.4, NF.1, NF.2: Collect data consisting of distance, intervals of time, volume, mass, or money. Read, interpret, and create line plots that communicate data stories where the line plot measurements consist of fractional units of measure. For example, create a line plot showing classroom or home objects measured to the nearest quarter inch.
Rectangle Investigations	Reasoning with Data	MD.1, MD.2, MD.3, MD.5, MD.6: Investigate rectangles in the world, measuring lengths and angles, collecting the data, and displaying it using data visualizations.
Number and Shape Patterns	Exploring Changing Quantities	OA.5, OA.1, OA.2, NBT.4: Generalize number and shape patterns that follow a given rule. Communicate understanding of how the pattern changes in words, symbols, and diagrams––working with multi-digit numbers.
Factors and Area Models	Exploring Changing Quantities	OA.1, OA.2, OA.4, NBT.5, NBT.6: Break numbers inside of 100 into factors. Illustrate whole number multiplication and division calculations as area models and rectangular arrays that illustrate factors.
Multi-Digit Numbers	Exploring Changing Quantities	NBT.1, NBT.2, NBT.3, NBT.4, OA.1: Read and write multi-digit whole numbers in expanded form and express each number component of the expanded form as a multiple of a power of ten.
Fraction Flexibility	Taking Wholes Apart, Putting Parts Together	NF.3, NF.1, NF.4, NF.5, OA.1: Understand that addition and subtraction of fractions as joining and separating parts that are referring to the same whole. Decompose fractions and mixed numbers into unit fractions and whole numbers, and express mixed numbers as a sum of unit fractions.
Visual Fraction Models	Taking Wholes Apart, Putting Parts Together	NF.2, NF.1, NF.3, NF.5, NF.6, NF.7: Use different ways of seeing and visualizing fractions to compare fractions using student generated visual fraction models. Use >, < and = to compare fraction size, through linear and area models, and determine whether fractions are greater or less than benchmark numbers, such as ½ and 1.
Circles, Fractions and Decimals	Taking Wholes Apart, Putting Parts Together and Discovering Shape and Space	NF.5, NF.6, NF.7, OA.1. MD.2, MD.5, MD.7: Understand, compare, and visualize fractions expressed as decimals. Recognize fractions with denominators of 10 and 100, e.g., 25 cents can be written as 0.25 or 25/100. Connect a circle fraction model to the clock face. Example 3/10 + 4/100 = 30/100 + 4/100 = 34/100
Shapes and Symmetries	Discovering Shape and Space	MD.5, MD.6, MD.7, G.1, G.2, G.3, NBT.3, NBT.4: Draw and identify shapes, looking at the relationships between rays, lines, and angles. Explore symmetry through folding activities.
Connected Problem Solving	Discovering Shape and Space	MD.1, MD.2, MD.3, NBT.3, NBT.4, NBT.5, NBT.6, OA.2, OA.3, G.3: Solve problems with perimeter, area, volume, distance, and symmetry, using operations and measurement.

Grade Five

In fifth grade, equivalence and flexibility are Big Ideas, with both particularly relating to operations and fractions. Using relationships in the world to make meaning out of multiplication, division, fractions, and estimation requires a great deal of exploration. Using portion sizes to estimate with fractions is helpful because thinking about portions is a useful and underdeveloped idea that gives fractions meaning and utility. At this grade, students work with powers of 10, use exponential notation, and can explain patterns in the placement of the decimal point when a decimal is multiplied by a power of 10.

Fifth-grade students are expected to fully understand the place value system, including decimal values to thousandths, building from the foundation laid in earlier grades. Ideas to help with decimal understanding include using base 10 blocks, with the 3-D cube representing one unit so that students have a tactile, visual model to consider the value of the small cube, the rod, and the 10 by 10 flat. In a virtual environment, students can use a Computer-Aided Design (CAD), Tinkercad, or other program to design and build complex shapes. While they are building 3-D representations in a 2-D space, it is important to ask students to think about what makes their 2-D drawings appear to be 3-D. Shapes in this environment may appear to be a parallelogram or a rhombus when they are representing a 3-D object—what the shape of the face really is in 3-D space is a square. Asking students to build their CAD designs out of cardboard or paper is a good way to have them explore the way shapes look when they change the angle of their view.

Another useful tool is a printed 10 by 10 grid. Students visualize the whole grid as representing the whole and can shade in various decimal values. Fifth-grade students use equivalent fractions to solve problems, so it is important that they have a strong grasp of equality and can use benchmark fractions (e.g., 1/2, 2/3, 3/4) to reason about, compare, and calculate with fractions. Experiences with placing whole numbers, fractions, and decimals on the same number line contribute to building fraction number sense. Students need time and opportunity to collaborate, critique, and reason about where to place the numbers on the number line.

When students in fifth grade conduct data investigations, they ask questions, collect data, analyze results, and communicate their findings. While the data visualizations included in the fifth-grade standards only include picture graphs, bar graphs, and line plots, students do not need to be restricted to these; data in the modern world is represented in many creative and non-standard ways, and it is important that students learn to read such data representations. Also, while standard data representations, such as bar graphs, show repeated measurements of a single varying quantity, science curricula in particular, and many questions of interest in general, require the consideration of relationships between two or more different changing quantities, such as erosion and time (Next Generation Science Standards [NGSS] 4-Earth and Space Science [ESS] 2-1 Earth’s Systems) or length or direction of shadows and time (NGSS 5-ESS1-2 Earth’s Place in the Universe). Such reasoning involves multiple variables, which is an important aspect of modern encounters with data that students experience. Although the scatter plot, a crucial data representation tool for two varying quantities, is not expected to be fully understood until later grades (8.SP.1), it can be explored informally much earlier for students to be prepared for middle school content. For example, students can plot quantities changing over time (e.g., height of a plant, length of the day, high temperature for the day), with time on the horizontal axis and the changing quantity on the vertical. Once such a plot is created, it is an excellent context for a “notice and wonder” discussion.

Moving to the fore in fifth grade are ideas about patterns and relationships in 2-D and 3-D space. Students begin to use the coordinate plane to represent and question relationships, and they begin to think about how to count and represent volume using cubic units. Providing investigations where students see volume as a visual model of unit cubes contained inside a 3-D shape is important work. Students have ample opportunities to study the volume of complex shapes, e.g., a pyramid, where they construct the volume as layers of unit cubes and grapple with the fractions of unit cubes that make up the volume. This is a way to further connect the meaning of a unit with fractions of a unit. In a virtual environment, students can build complex shapes in Tinkercad or other similar apps. Ask students to create and then hand draw their designs since this will engage different areas of their brain. If students are building complex 3-D designs virtually in a CAD space, it is a good idea to ask them to try to construct their designs outside of the computer environment. Ask if they can construct their shape out of cardboard or paper. Was it possible to build the shapes they had drawn? What challenges did you face?

Students who are ELs are encouraged to use their developing English and native language assets (e.g., cognates, morphological awareness) and draw on their prior knowledge. Teachers can examine text and tasks for key language forms and structures, and general as well as discipline-specific, high-utility academic vocabulary words linked to the Big Ideas and connections. Teachers can provide purposeful scaffolds and supports to engage EL students in sustained mathematical discourse in multiple contexts to build academic language and knowledge. Planned and “just-in-time” scaffolds and supports provide multiple entry points for meaning making and sharing of ideas in mathematical ways and include representations, expression starters and builders, and targeted and high-utility academic vocabulary and language structures (e.g., problems, explanations, arguments, descriptions, procedures). Teachers guide deconstruction and/or co-construction of problems, investigations, arguments, explanations, descriptions, methods, and connections.

Critical Areas of Instructional Focus for Grade Five

Figure 7.4. Grade Five Big Ideas (Figure 6.56 in the 2023 CA Mathematics Framework)

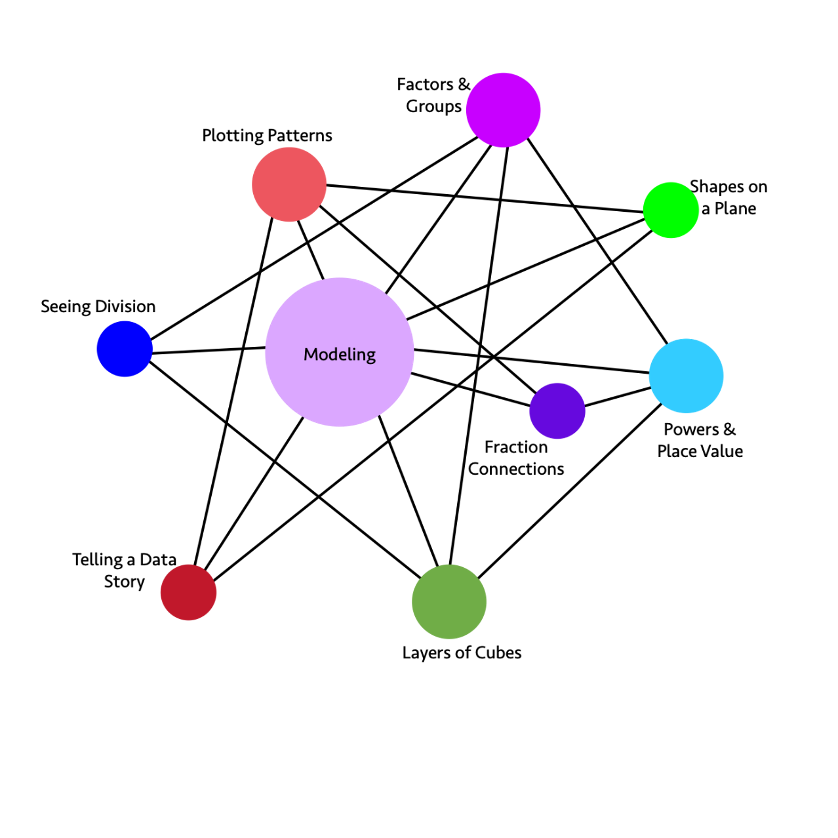
Long description: The graphic illustrates the connections and relationships of some fifth-grade mathematics concepts.

Direct connections include:

• Factors and Groups directly connects to: Powers and Place Values, Layers of Cubes, Modeling, Seeing Division
• Shapes on a Plane directly connects to: Telling a Data Story, Modeling, Plotting Patterns
• Powers and Place Value directly connects to: Layers of Cubes, Fraction Connections, Modeling, Factors and Groups
• Layers of Cubes directly connects to: Powers and Place Value, Factors and Groups, Modeling, Seeing Division
• Telling a Data Story directly connects to: Shapes on a Plane, Modeling, Plotting Patterns
• Seeing Division directly connects to: Layers of Cubes, Modeling, Factors and Groups
• Plotting Patterns directly connects to: Telling a Data Story, Modeling, Fraction Connections, Shapes on a Plane
• Fraction Connections directly connects to: Powers and Place Value, Modeling, Plotting Patterns
• Modeling directly connects to: Plotting Patterns, Factors and Groups, Shapes on a Plane, Powers and Place Value, Fraction Connections, Layers of Cubes, Telling a Data Story, Seeing Division

Figure 7.4a. Grade Five Big Ideas, Content Connections, and Content Standards (Figure 6.57 in the 2023 CA Mathematics Framework)

Big Ideas	Content Connections	Grade Five Content Standards
Plotting Patterns	Reasoning with Data	G.1, G.2, OA.3, MD.2, NF.7: Students generate and analyze patterns, plotting them on a line plot or coordinate plane, and use their graph to tell a story about the data. Some situations should include fraction and decimal measurements, such as a plant growing.
Telling a Data Story	Reasoning with Data and Exploring Changing Quantities and Discovering Shape and Space	G.1, G.2, OA.3: Understand a situation, graph the data to show patterns and relationships, and to help communicate the meaning of a real-world event.
Factors and Groups	Exploring Changing Quantities	OA.1, OA.2, MD.4, MD.5: Students use grouping symbols to express changing quantities and understand that a factor can represent the number of groups of the quantity.
Modeling	Exploring Changing Quantities	NBT.3, NBT.5, NBT.7, NF.1, NF.2, NF.3, NF.4, NF.5, NF.6, NF.7, MD.4, MD.5, OA.3: Set up a model and use whole, fraction, and decimal numbers and operations to solve a problem. Use concrete models and drawings and justify results.
Fraction Connections	Exploring Changing Quantities and Taking Wholes Apart, Putting Parts Together	NF.1, NF.2, NF.3, NF.4, NF.5, NF.7, MD.2, NBT.3: Make and understand visual models, to show the effect of operations on fractions. Construct line plots from real data that include fractions of units.
Seeing Division	Taking Wholes Apart, Putting Parts Together	MD.3, MD.4, MD.5, NBT.4, NBT.6, NBT.7: Solve real problems that involve volume, area, and division, setting up models and creating visual representations. Some problems should include decimal numbers. Use rounding and estimation to check accuracy and justify results.
Powers and Place Value	Taking Wholes Apart, Putting Parts Together	NBT.3, NBT.2, NBT.1, OA.1, OA.2: Use whole number exponents to represent powers of 10. Use expanded notation to write decimal numbers to the thousandths place and connect decimal notation to fractional representations, where the denominator can be expressed in powers of 10.
Layers of Cubes	Discovering Shape and Space	MD.5, MD.4, MD.3, OA.1, MD.1: Students recognize volume as an attribute of three-dimensional space. They understand that a 1-unit by 1-unit by 1-unit cube is the standard unit for measuring volume. They decompose 3-D shapes and find volumes of right rectangular prisms by viewing them as decomposed into layers of arrays of cubes.
Shapes on a Plane	Discovering Shape and Space and Exploring Changing Quantities	G.1, G.2, G.3, G.4, OA.3, NF.4, NF.5, NF.6: Graph 2-D shapes on a coordinate plane, notice and wonder about the properties of shapes, parallel and perpendicular lines, right angles, and equal length sides. Use tables to organize the coordinates of the vertices of the figures and study the changing quantities of the coordinates.

---

Sources

[1] University of Cambridge NRICH Program (https://nrich.maths.org/)