Chapter 4 provided information about digital learning in mathematics. The purpose of Chapters 5-9 is to present standards and instructional guidance to support the continuum of learning from TK/K through grade 10. These chapters prioritize critical areas of instructional focus by grade levels. Attention to these critical areas will ensure that students transition to the next grade level well prepared to learn new skills and concepts. This guidance serves as a companion resource to the California Common Core State Standards: Mathematics and the Mathematics Framework. The organization of the content and practice standards as “big ideas” raises the individual standards to a higher level of “big ideas” and highlights the importance of the content and the ways it is connected to other content and practices. The standards guidance is intended to support teachers as they implement math instruction in online, blended, or in-person learning environments.
California’s goal for all students is that they learn mathematics as a meaningful subject of connected ideas. Teaching with meaning and connections requires a different organization of content and practice standards. The Mathematics Framework advocates for teaching to “big ideas” rather than organizing teaching around the small descriptions of mathematics set out in the standards. Mathematics professor Randy Charles defines a big idea as a “statement of an idea that is central to the learning of mathematics, one that links numerous mathematical understandings into a coherent whole” (Charles & Carmel, 2005, p.10). A “big idea” approach has been shown by research to engage students and increase achievement (Boaler et al., 2021; Cabana et al., 2014, Makar, 2018). The approach raises the individual standards to a higher level of “big ideas” that show teachers and students the importance of the content and the ways it is connected to other content and practices. As teachers orient their approach to big ideas and connections, they will find that there seems to be less content to teach and more time for students to explore ideas and learn deeply. The same content is actually taught and learned, but the organization of connections and big ideas allows for a more coherent approach in which students learn different, connected ideas together. The Mathematics Framework has organized Content Connections (CCs) of “Communicating stories with data,” “Exploring changing quantities,” “Taking wholes apart and putting parts together,” and “Discovering shape and space,” and this document organizes the big ideas under these broad content headings, which are explained in more detail below. Each grade band section (TK-2, 3-5, 6-8, 9-10) shows the progression of big ideas across the grades.
The Mathematics Framework includes a principle that mathematics learning in classrooms should always have a purpose and that rather than students working through questions without mathematical direction, they should work on an approach of “investigating and connecting.” To do this, the Framework recommends “crosscutting drivers of investigation” that can guide investigations. The drivers are:
- Making sense of the world (understand and explain),
- Predicting what could happen (predict), and
- Impacting the future (affect).
Figure 5.1 shows these drivers and the ways they can be applied to any combination of content and mathematical practices.
Figure 5.1. The Drivers of Investigation, Content Connections, & Mathematical Practices from the Mathematics Framework.
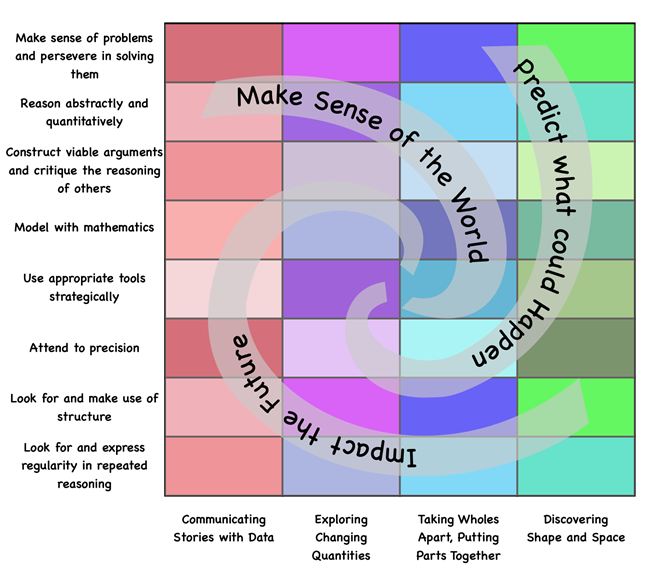
Long description: Three Drivers of Investigation (DIs) provide the “why” of learning mathematics: Making Sense of the World (Understand and Explain); Predicting What Could Happen (Predict); Impacting the Future (Affect). The DIs overlay and pair with four categories of Content Connections (CCs), which provide the “how and what” mathematics (CA-CCSSM) is to be learned in an activity: Communicating stories with data; Exploring changing quantities; Taking wholes apart, putting parts together; Discovering shape and space. The DIs work with the Standards for Mathematical Practice to propel the learning of the ideas and actions framed in the CCs in ways that are coherent, focused, and rigorous. The Standards for Mathematical Practice are: Make sense of problems and persevere in solving them; Reason abstractly and quantitatively; Construct viable arguments and critique the reasoning of others; Model with mathematics; Use appropriate tools strategically; Attend to precision; Look for and make use of structure; Look for and express regularity in repeated reasoning.
Big Ideas and Network Maps
The California Common Core State Standards: Mathematics offer domains, cluster headings, and standards – with most textbook publishers translating the detailed standards into short, procedural questions. A problem with working through standards and associated questions is that teachers do not have time to go in depth on any of the standards, or even to teach them all. A different approach is to consider the big ideas, as set out in the introduction to this section, that bring in many different standards, that often go across the clusters and domains. As students work on rich tasks, they will encounter many of the standards but in a more connected and meaningful way. This document sets out this “big idea” approach to mathematics, with the goal of helping teachers and their students, both during a period of decreased learning time and moving forward.
To highlight mathematical connections, each grade has a network map which shows the big ideas as nodes. These represent important and foundational content, and an ideal approach to teaching mathematics, in person or online, starts with choosing rich tasks that focus on the big ideas.1 As students explore and investigate with the big ideas, they will likely encounter many of the different content standards and see the connections between them.
The size of the node relates to the number of connections it has with other big ideas. The connections between big ideas are made when the two connected big ideas contain one or more of the same standards. The big idea colors in the nodes correspond to the table where the big ideas are correlated with full descriptions. The descriptions of each big idea are not taken from the standards or the clusters or domains; rather, they are new descriptions, as many of the ideas go across clusters and domains. For example, in grade 3 the big idea: Fractions of Shape & Time, brings together standards from the domains of Measurement and Data, Number and Operations in Base Ten, Fractions and Geometry. The new descriptions integrate well with the mathematical practices, as they describe mathematics as a subject of reasoning and communicating. The approach is illustrated through three vignettes, at grades 4, 8, and Integrated 2.
Grade Four Vignette
Teaching to Big Ideas
Perplexing Measures (Boaler, Munson, & Williams, 2017)
In this lesson, students encounter the big idea of “Measuring and Plotting,” which includes standards from the domains of Number and Operations – Fractions and Measurement and Data. The activity supports learning inside the Standards of Mathematical Practices; 1. Make sense of problems and persevere in solving them, 2. Reason abstractly and quantitatively, 3. Construct viable arguments and critique the reasoning of others, 4. Model with mathematics, 5. Use appropriate tools strategically, and 6. Attend to precision.
Ms. Kamala wanted her fourth grade students to experience measurement in a creative way and understand the idea of measuring with different units. She chose to use an activity called Perplexing Measures from Mindset Mathematics, Grade four. Ms. Kamala began the lesson by asking students to make and name their own unit of measure. Each group was given a different length of adding machine tape and told that it had a length of 2 whole units. Students learning in a virtual setting can find or piece together a long piece of paper that is around 3 inches wide and greater than two feet long. Students estimate the length and width instead of measuring exactly with a ruler or yardstick. The students in Ms. Kamala’s class folded their strip of paper tape into 16 equal increments by halving after each fold. After they completed folding, they stretched out their measure strip and labeled the increments, counting by eighths. They continued counting by different unit measures, whole numbers, quarters, and halves so the different representations of equivalent fractions were shown on their strip.
Figure 5.2. Adding Machine Tape Folded in Half 8 Times to Produce 16 Equal Units

In one of the groups the students labeled their measuring strip a “Zoomboogle.”
Figure 5.3. Measure of One Zoomboogle Is Approximately 71 Centimeters Long

Students were asked to measure different items and record the measure to the nearest eighth of a unit.
Figure 5.4. Student Measure of a Tangram Structure and a Stuffed Black Cab Toy


The tangram structure measures close to one quarter of a Zoomboogle, and the black cab measures about three-eighths of a Zoomboogle. Students measured and recorded different objects approximating their measures to the nearest eighth.
After students completed measuring and recording lengths of objects, Ms. Kamala asked them to make a measurement display of the objects they measured with a table showing the objects and the measured length. Students in a virtual setting could collaborate inside of a Google Sheet where they enter each item measured in one column and in another column enter the measure they determined using their personal measuring tape. Another option for students in a virtual setting would be to add images of what they are measuring in Google Slides presentation that can be shared with the class. In Ms. Kamala’s class, groups of students moved around the room to the different displays and verified the measures of the objects using the measuring strip the group had created. Students left notes with questions and feedback for the other groups. Many students commented on the creative names the students used for their measuring strip, while others questioned the estimated value of the measure that was recorded. Still others asked why an object was measured by the dimension that was chosen: “Why did you measure the height of the desk and not the length or width?” After groups had a chance to review the comments and questions left for them, Ms. Kamala began a class discussion by asking, “What challenged you in this activity? How did you respond to that challenge?” She pays particular attention to students who are English learners, highlighting the mathematics vocabulary of words like height, length, and width. Students reflected on their challenges, which centered around measuring to the nearest eighth of a unit and having to estimate the length. Students discussed how they estimated the length and their method for choosing whether to over or underestimate the value.
Finally, Ms. Kamala displayed their different measuring strips and asked them to discuss what they noticed. In a virtual setting, students can make a Google Slides presentation with images showing the items they measured next to their personal measuring strip. Ms. Kamala placed a couple of examples of items measured next to the displayed strips and asked them to discuss the different measures for the same item. Ms. Kamala asked, “We all measured and used the same process to develop our measuring strip. If we measure the same object with two different measuring strips, will the measurements be the same?
Figure 5.5. Sample Student Work

Ms. Kamala encouraged her students to give convincing arguments and to listen carefully to each other, which also provided rich language learning opportunities. Model sentence frames were provided (offering additional support for English learners and other students needing that support), and the teacher dedicated individual and small-group time to ensure student comprehension and to provide oral coaching of the sentence frames. To conclude the activity, Ms. Kamala asked students to write in their journals. The prompt she gave them was: “How are fractions useful when measuring an object?”
Grade Eight Vignette
Teaching to Big Ideas
This activity from the Mathematics Framework includes the grade 8 big idea: “Interpret scatter plots,” which includes standards from the different domains, of “Statistics and probability,” “Expressions and equations,” and “Functions.” It also connects to other big ideas, such as “Data graphs and tables,” “Data explorations,” and “Linear equations.” The low-floor/high-ceiling nature of the task means it could also be used in high school courses of algebra 1 and integrated 1. The activity supports learning inside the Standards of Mathematical Practices: 1. Make sense of problems and persevere in solving them, 2. Reason abstractly and quantitatively, 3. Construct viable arguments and critique the reasoning of others, 4. Model with mathematics, 5. Use appropriate tools strategically, 6. Attend to precision, and 7. Look for and make use of structure. This activity can easily be conducted online, with students drawing from different technology tools as they work.
Investigating Mammals. Grade 8.
Students are introduced to the Common Online Data Analysis Platform (CODAP), a website providing free educational software for data analysis. After a brief introduction to the technical capabilities of CODAP and a review of terms and concepts to help English learners, students are invited to explore a CODAP database of 27 mammals. The database provides variables, such as the height, mass, speed, life-span, and sleep hours of the mammals. The students quickly become curious and ask questions such as, “Do bigger animals sleep longer?” They plot the two variables with the graph tool and start to notice a relationship; contradictory to what they thought, it seems the bigger animals sleep less. The students start an animated conversation discussing the reasons this might be: “Is it because they are more likely to be predators?” They then move on to investigate another relationship—who sleeps more, plant or animal eaters? The students again notice a relationship as well as an outlier (the rabbit), so they wonder about the rabbit and look at more rabbit data. The students’ investigation of bivariate data and their relationships is filled with moments of curiosity and excitement, as well as important learning. Before concluding the lesson, the teacher dedicates individual and small-group time with the EL students to ensure comprehension and to answer any questions. This activity is well positioned for virtual exploration by students working in small groups. Groups can meet in a Google Hangout room together to discuss and share their findings while they are each working inside the online CODAP data set.

Long description: Sample student data collection board with sticky notes, charts, and pictures. One sticky note has the student names. Another sticky note shares one of the students’ question: Do big animals sleep more than small animals? The students answer this question in another sticky note, saying that their graph shows that some of the biggest animals sleep the least. In another sticky note, students ask a second question: do plant eaters sleep less than meat eaters? They answer this in another sticky note that says: Yes! We can see that almost all plant eaters represented sleep less on average. Three more sticky notes share other data findings about the rabbit— One says: the rabbit is small in mass and sleeps an average amount compared to other mammals. Another says that when comparing the rabbit to other plant eaters it stands out for sleeping much more. And a third says: There is one animal smaller than the rest in the plant eaters that sleeps a lot more – the animal is a rabbit. The students also share graphs that show the different relationships they investigated (sleep v. diet, mass v. sleep and diet v. sleep).
Grade Ten Vignette
Teaching to Big Ideas
Vignette from Integrated Course 2: Cable Ready – from high school teachers Lisa Doak, Sally Collins, and Kenny Reisman, from the Interactive Mathematics Program (IMP).
This is an activity that satisfies IM2 big idea: “Equations to predict and model,” which includes standards from the different domains: “Creating equations,” “Reasoning with equations and inequalities,” “Interpreting functions,” “Building functions,” and “Arithmetic with polynomials and rational expressions.” Depending on the directions students decide to take the investigation, the task may also address the big idea of “Circle relationships” and the domain of “Circles,” or the big idea of “Trig Functions” and the domain of “Trigonometric Functions.” The activity supports learning inside the Standards of Mathematical Practices: 1. Make sense of problems and persevere in solving them, 2. Reason abstractly and quantitatively, 3. Construct viable arguments and critique the reasoning of others, 4. Model with mathematics, 5. Use appropriate tools strategically, 6. Attend to precision, 7. Look for and make use of structure, and 8. Look for and express regularity in repeated reasoning.
Activity: Cable Ready
When Madie and Clyde bought their orchard, a straight electrical cable ran along the ground from the center of the orchard, at (0, 0) in their coordinate system, to the point (30, 20).
1. They wanted to start their planting while they waited for the electrical company to move the cable safely underground, but they had to be sure not to plant trees right on the cable. Keep in mind that Madie and Clyde plant trees at every lattice point in the orchard.
Could they plant a complete mini-orchard of radius 1 at the center of their lot without planting right on the cable?
b. Answer the same question for a mini-orchard of radius 2.
c. What is the radius of the biggest complete mini-orchard Madie and Clyde could plant without planting on the cable? Assume the tree trunks are very thin.
2. Suppose Madie and Clyde plant the biggest possible mini-orchard from Question 1c. How big will the tree trunks have to become before one of them bumps into the cable? With your group, prepare a presentation that summarizes your work on Question 2 for presentation to the class. (Interactive Mathematics Program, Activate Learning)
Mathematically, students are trying to find the distance from a point to a line. In this example, they are trying to find the radius of the circle which is tangent to the line AB. In a virtual setting, students can work together in small groups organized in a breakout room. They can work together discussing their strategies and working towards creative solutions using DESMOS or other geometric software.
Figure 5.7. A Visual Representation of the Problem
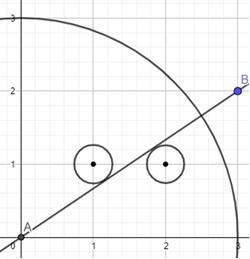
Students have presented several different methods for solving the problem. A sample of those methods are provided below:
(1) Algebraic: As shown in Figure 5.8, students find the equation of the line represented by the cable and then find the equation of the line perpendicular to it through the point (1, 1). They then find the intersection point of those two lines by solving a system of equations. Finally, they find the distance between that intersection point and the center of the tree at (1, 1).
Figure 5.8. An Algebraic Solution
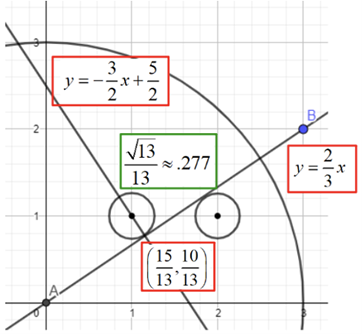
Long description: An algebraic solution to the problem shown visually. A quarter circle is drawn with center at the origin labeled point A with a radius of 3 units. A line is drawn from the origin and through point B located at (3,2). The equation of Line AB is y equals two-thirds x. Another line is constructed through a point located at 15 thirteenths and 10 thirteenths that is perpendicular to line AB. The equation of this line is y equals negative three halves x plus five halves.
(2) Geometric: As shown in Figure 5.9, students use similar triangles found with alternate interior angles of parallel lines, as well as the Pythagorean Theorem, to find the hypotenuse of the larger triangle. The .5 length is established by showing that any line through the midpoint of a segment connecting 2 points is equidistant from the 2 points.
Figure 5.9. A Geometric Solution
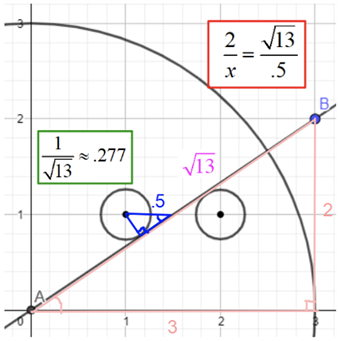
Long description: A geometric solution to the problem shown visually. It shows a quarter circle with center at (0,0) and a radius of 3 units. A line is drawn from the origin to point B at point (3,2). The hypotenuse of the triangle formed by points A,B has a radius of square root of 13.
(3) Trigonometric: As shown in Figure 5.10, students use alternate interior angles of parallel lines for congruent angles.
Figure 5.10. A Trigonometric Solution
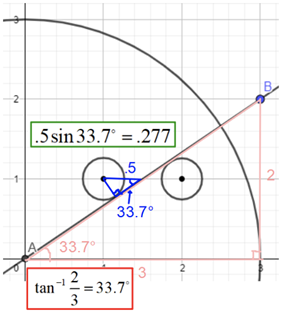
Long description: A trigonometric solution to the problem shown visually. A quarter circle is drawn with center at the origin and labeled point A with a radius of 3 units. A line is drawn from the origin and through point B located at point (3,2). A triangle is constructed from points A, B and a point at (3,0). A circle is drawn with center at point (1,1) with a point on the circle tangent to line AB. A triangle is constructed showing the distance from the circle perpendicular to line AB is .277.
Mathematics through the Key Themes of ELA/Literacy and English Language Development
The relationship between this document and the key themes of the ELA/ELD Framework, can be found in these areas:
Meaning Making: Mathematics, as a lens and a language, has meaning and sense-making as its central purpose. As a lens, mathematics brings patterns, connections, and relationships into focus, allowing students to describe, inspect, and, in many cases, apply these relationships in novel contexts, expanding mathematical knowledge in infinite directions. Mathematics is integral to understanding important human endeavors, such as public health, economic growth, and sustaining the environment, among many others. The recommendation of the Mathematics Framework is that teachers give mathematics problems to students that encourage them to investigate and connect ideas, through the three drivers of investigation shown in Figure 5.1. These drivers give mathematics purpose, as they invite students to use mathematics to understand and explain the world, to describe patterns that can help predict what comes next, or to consider a range of actions to impact the future. Meaning and sense-making is an active process for learners that is intellectually satisfying, propelled by challenging mathematics tasks, supportive instruction, and opportunities to use a full range of classroom and language resources, including collaborators and tools.
Foundational Skills: A foundational skill in mathematics is flexibility. In the area of numbers, the foundational skill is not rote memorization of number facts, but rather numerical flexibility, which leads to number sense (Boaler, 2016). As students learn to investigate with numbers by composing and decomposing numbers, and using different strategies, they learn to make sense of the base-10 number system. The same flexibility is developed with symbol sense in algebra, thinking visually in geometry, and data sense in data science, and onwards. Flexibility allows students to orient themselves and navigate within mathematical terrains.
Language Development: Like all disciplines, mathematics has its own specialized system of encoding and communicating its concepts, knowledge, and understandings over time. This system includes words, numbers, symbols, graphs, diagrams, and, increasingly, many other forms of visual displays. Knowing a term or expression is to have a clear understanding of how to use it in a particular context and be aware of its relationship to other words. For students, and in particular for EL students, it is useful to identify and develop the high-utility academic vocabulary within units of study. Students can also be provided opportunities to utilize their native tongue when they are initially learning concepts (see also Gutierrez, 2018). Teachers can build understanding of how these words are enacted, defined, and used in mathematical ways, text, and tasks over time. Academic vocabulary includes general abstract words used across disciplines (e.g., compare, measure, evaluate, analyze, induce, deduce), abstract discipline-specific words (e.g., proportionality, equivalency, function), and technical discipline-specific words (e.g., variable, diameter, volume, cube, monomial, segment, numerator, hypotenuse). To engage in effective disciplinary discourse and produce using the mathematical register, students need multiple experiences with the forms and structures of the discipline’s genres: problem solving, argument, explanation, and procedure. Teachers can support students who are English learners by examining the language demands and language opportunities of texts and tasks and by guiding the deconstruction and/or co-construction of text and tasks for a particular purpose. Over time, students learn to read and write using the particulars of grammar and syntax of mathematics conventions, while also inventing their own representations, visuals, and inscriptions to express their emerging ideas. In this way, students develop their own mathematical voice and mathematical perspective, which they use to express themselves.
Effective Expression: While outdated stereotypes cast mathematics as a solitary enterprise, mathematics is continually built from and with a community of learners. By participating in classroom communities, for example, students learn to express themselves mathematically in a variety of forms. Reasoning is at the heart of the discipline of mathematics, and students learn to reason when they share their emerging ideas with each other, justify their thinking, act as skeptics for each other, and defend their methods and approaches. Classrooms are effective when teachers encourage students to share their conjectures, or mathematical ideas that students are not yet sure about, which other students can then discuss. Teachers can increase the level of expression for students who are linguistically and culturally diverse learners of English by strategically grouping them with peers who support and/or enhance their sharing of emerging ideas using their language assets, providing purposefully planned and “just-in-time” scaffolds for sustained communications, making explicit the academic language goals, and supporting the development and use of academic vocabulary (general, abstract, and technical discipline-specific). Mathematical communication is an important part of all mathematical work, in employment and in the discipline of mathematics. As students learn to formulate conjectures and then set out to explore and explain their ideas with increasing detail and examples, such as cases, they will learn mathematical communication. As ideas take shape, students may also develop models and arguments to engage stakeholders, audiences, and skeptics. When ideas have sufficiently matured, students may formalize their ideas in the form of proof, constructing a logical chain of reasoning that is validated by the members of the mathematics community. Proofs and other forms of derived results become the basis of new conjectures.
Content Connections in the Mathematics Framework
The big ideas set out in this document have been organized according to the Content Connections (CC) of the Mathematics Framework. Each of these CCs is outlined below:
CC1. Communicating Stories with Data
Data is all around, and an important goal for teachers is helping their students develop data literacy so that they can read and understand data in the world. In the older grades, this develops into an understanding of the important new discipline: data science. In the younger grades, students learn to identify data, measure and classify objects, and make and read data visualizations. In the middle grades, students learn to reason with data using statistical methods, collecting and using data from their lives, and continuing to interpret and make data visualizations. In the high school years, students continue to reason about and with data, and many of the algebraic concepts students learn, particularly functions, can be learned through data investigations. This area of mathematics lends itself to integration of mathematics with other disciplines, such as science and social sciences, as well as with data students meet and care about in their lives. It also provides extensive opportunities to show how mathematics and data science can be utilized to address social injustices and inequities, as students investigate topics such as redlining voter suppression, wealth gaps, food insecurity, agriculture, the environment, and healthcare (Berry III et al., 2020; Gutstein, 2007).
The Mathematics Framework defines data science:
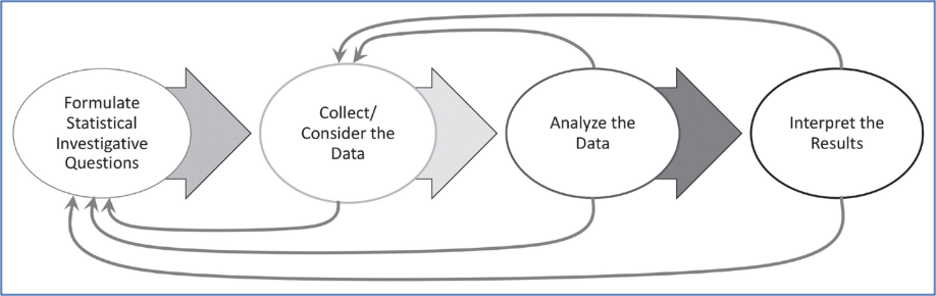
Data Science is the process of uncovering the stories hidden within data. It involves collecting, cleaning, wrangling, analyzing, and visualizing data (that is often massive in size) to uncover patterns and trends and communicate them to others. Professional data scientists draw upon mathematics, statistics, and computer science, and think critically about the qualitative features of a data set to find meaning and communicate the results of their inquiries. Data scientists work together to address uncertainty in data while avoiding bias. The terms statistics and data science both refer to the processes and tools of finding meaning in data, and some people use them interchangeably. Statistics traditionally uses theoretical tools to build and evaluate proposed mathematical models, using data from a population of interest. Data science highlights the expansion in computing and visualization tools that have made many more techniques available for finding meaning in data—many relying on innovative visualizations of data that enable major features to be spotted and explored further. Because statistics has become synonymous in much of TK-12 education with a very limited set of procedures (mean, median, standard deviation, interquartile range, correlation, and linear regression, along with a few data visualizations, such as line plots and scatter plots), this Framework uses data science to emphasize the full statistical and data science investigation process (see Figure 5.12). Students experience statistical tools in the process of investigating authentic questions.
Figure 5.12. The statistical and data science investigation process, from GAISE 2020 (Franklin & Bargagliotti, 2020)
CC2. Exploring Changing Quantities
One of the most powerful uses of mathematics in school and in the world is making sense of change. In the early grades, students are fascinated to learn that adding to a group of objects gives a different number and that the number can be arrived at in many different ways. As students learn number flexibility and number sense, they will learn to change numbers through the use of different operations, such as addition, subtraction, multiplication, and division. They will also learn about the ways mathematics can be applied to changed quantities in the world (e.g., weight, length, value, and in later grades, speed, and acceleration). Mathematicians must find ways to represent the relationships between quantities in order to make sense of and model complex situations. To explore and make sense of changing quantities is an important area of mathematics that applies across mathematical grades and situations.
CC3. Taking Wholes Apart, Putting Parts Together
An important practice that is a tool for the solving of most mathematical problems is the act of breaking a large problem into smaller parts, which are investigated, solved, then put back together into a whole. All mathematical content can be considered in this way; in this document, and within the Mathematics Framework, the content chosen provides particular insights when it is decomposed into manageable pieces and then re-assembled. When an investigation is included in this area, it is crucial that decomposing and re-assembly is a student task, not one that is taken on by a teacher or a textbook. As students learn to “take wholes apart and put parts together,” they will learn an important mathematical approach to the solving of complex problems.
CC4. Discovering Shape and Space
Visual thinking is an essential part of mathematics, as it helps all students learn and develop important brain connections (Boaler, 2019) and can be encouraged in all mathematical investigations. In all grades, it is important to realize that “visual thinking” or “geometric reasoning” is as legitimate as algebraic or computational thinking. In the early grades, students describe their worlds using geometric ideas, taking time to explore the nature of shapes and spaces in the world. As students move through the grades, they should continue this focus, also breaking shapes apart, and combining them, and relating them to measurement. Three-dimensional visualization and modeling are important 21st century understandings intrinsic to many jobs. Geometry software helps this area of mathematics come to life and is especially important in the high school years. The Mathematics Framework supports visual thinking by defining congruence and similarity in terms of dilations and rigid motions of the plane, and emphasizing physical models, transparencies, and geometry software.
Number Talks through the Grades TK–12
Number sense—the ability to use, adapt and think flexibly with numbers—is an important mathematical foundation and a precursor to higher level mathematics achievement. Number sense is a “big idea” that extends across all of the grades. A pedagogical practice that is highly effective for encouraging number sense is a “number talk,” sometimes referred to as a “math talk” and related to the practice of a “number string.” These can be used with students of all grade levels, including college students. The structure of a number talk is the following: The teacher gives a number problem to the class of students and asks students to think, mentally, about a way to solve it, without pen and paper. The teacher then asks for the different answers that may be produced and asks students to defend their answers using mathematical reasoning. Teachers can engage EL students in number talks by providing purposeful sentence frames and open-ended questions to build extended conversations, build fluency, and encourage struggle, which is important for brain development. Number talks provide powerful language models for EL students. This structure may be adapted in different ways. For example, students can turn and talk to partners before sharing their solutions. Students who are English learners are encouraged to use their language assets in English and native languages and might be partnered with peers accordingly. As students are using language to convey mathematical ideas, it helps with the development of language and reasoning as set out in the California English Language Development (CA ELD) Standards. In the course of a number talk, students often adopt methods that another student has presented that make sense to them. Number talks, designed to highlight a particular type of problem or useful strategy, serve to advance the development of efficient, generalizable strategies for the class. These class discussions provide an interesting challenge, and teachers can create a safe place in which students can explore, compare, and develop strategies.
Effective number talks can advance students’ capacity for collaborative, interpretive, and productive communication, helping them develop a positive mathematical identity. They show something important – that mathematics problems can be approached in different ways; they highlight mathematical creativity, and they support the development of number sense. Number talks also integrate mathematics content and mathematical practices, especially Standards collaborative for Mathematical Practice (SMP) 2, 3, 4, 6, 7, and 8.
Number talks can be enacted using technology during distance learning. A teacher can put the number problem on a Jamboard or other interactive white board space, and ask the class to share their thinking, recording the student work onto the Jamboard. The following examples include excerpts from the Mathematics Framework.
Number Talks TK–2
Several types of number talks are appropriate for grades TK–2. Some possibilities include the following:
- Dot talks: A collection of dots is projected briefly (just for a few seconds), and students explain how many they saw and the method they used for counting the dots. A teaching example can be seen at this link.2
- Ten frame pictures: An image of a partially filled 10-frame is projected briefly, and students explain various methods they used to figure out the quantity shown in the 10 frames.
- Number problems: Written in horizontal format, either an addition or subtraction problem is presented, involving numbers that are appropriate for the students’ current understanding. Presenting problems in horizontal format increases the likelihood that students will think strategically rather than limit their thinking to an algorithmic approach. For example, first graders might solve 7 + ? = 11 by thinking “7 + 3 = 10, and 1 more makes 11.” Second graders subtract two-digit numbers. To solve 54 – 25 mentally, they can think about 54 – 20 = 34, and then subtract the 5 ones, finding 34 – 5 = 29.
Number Talks 3-5
Number talks in grades 3–5 can strengthen, support, and extend place value understanding, calculation strategies, and fraction concepts.
Some examples of problem types might include the following:
- Students can perform multiplication calculations using known facts and place value understanding and apply properties to solve a two-digit by one-digit problem. For example, if students know that 6 x 10 = 60 and 6 x 4 = 24, they can calculate 6 x 14 = 84 mentally. Presenting such calculation problems in horizontal format increases the likelihood that students will think strategically rather than limit their thinking to an algorithmic approach.
- Students can use relational thinking to consider whether 42 + 19 is greater than, less than, or equal to 44 + 17, and explain their strategies.
- Asking students to order several fractions mentally encourages the use of strategies, such as common numerators and benchmark fractions. For example, students can arrange in order, least to greatest, and explain how they know: 4/5, 1/3, 4/8.
Number Talks 6-8
In grades 6–8, number talks can include a focus on order of operations, and involve irrational numbers, as well as percents and decimals.
Some examples of problem types for Math Talks at the 6–8 grade level might include the following:
- Order of operation calculations allow students to apply properties to help simplify complicated numerical expressions. For example, 3(7 – 2)^2 + 8 ÷ 4 – 6 x 5.
- Students can use operations involving irrational numbers to ask the following questions: “2/3 of pi is approximately how much?” and “Four times sqrt(8) is closest to which integer?”
- Students can solve percent and decimal problems, reflecting on the following questions: “What is 45% of 80?,” “Calculate the percent increase from 80 to 100,” or “0.2% of 1000 is how much?”
Number Talks 9–12
Number talks in grades 9–12 can strengthen, support, and extend algebraic simplification strategies involving expressions, connect algebra concepts to geometry, and provide opportunities to practice estimation of answers. Also, many number talks from grades 6–8 (see previous section) are still readily applicable in grades 9–12, as they can lay valuable groundwork for algebraic understanding. For example, strategies that make use of place value and expanded form of multiplication problems, such as 134 times 36, can be employed to understand multiplication of binomials.
Some examples of number talks appropriate for grades 9 and upwards include the following:
- Which graph doesn’t belong? Various collections of graphs could be used, where all but one graph agree on various characteristics. The ensuing conversations help students attend to precision in the graphs and with their language (SMP.6) as they talk out the underlying causes of the differences between the graphs. For example, four graphs of polynomial functions could be displayed, with three odd-degree polynomial and one even-degree polynomial, which can highlight the notion of how the terms even and odd are used with regard to polynomials. Another example could be where one function displayed has multiple real roots, while the others have single or no real roots.
- Students can rewrite expressions using radical notation. There are often multiple approaches to simplifying expressions, so these can serve as excellent discussion points for students to see a variety of ways to approach simplification.
- Similarly, there is merit in sharing and discussing the myriad of ways to approach multiplying monomials, binomials, and trinomials (e.g. (x+y)(3x-2y)), including algebraic properties, such as the distributive property and generic rectangles.
Number Talk Resources
Some additional number talk resources include, but are not limited to, the following:
- San Francisco Unified School District has compiled a comprehensive page of resources for using Number Talks.3
- Inside Mathematics includes video examples of number talks from classrooms, grade one through grade seven.4
- Activities, videos, and research findings for number talks can be found on YouCubed,5 a website that includes a page with resources dedicated to number sense and number talks.6
Data Talks TK-12
Like “number talks,” data talks offer a short pedagogical routine to help students develop data literacy. Instead of sharing a number problem, teachers can show a data visualization and ask students open questions such as “What do you notice?” or “What do you wonder?” or “What is going on in this data visualization?” Students can be engaged with real data from the world, and it is an ideal opportunity to help develop awareness of social justice issues. Teachers can encourage student noticing and questions, without needing to have knowledge of the topic of the data visualization. The idea of a data talk was inspired by a New York Times weekly section called, “What’s Going on in this Graph?” in collaboration with the American Statistical Association. If teachers cannot answer student questions, they can model the important practice of being comfortable with uncertainty and being curious to find out more. The New York Times data visualizations are mainly suitable for students in middle school and older grades. For students from the TK-12 grades, YouCubed shares several “data talks.” Many of the data visualizations illustrate how multiple variables can be incorporated into one graphic, which allows students to think in multivariable ways.
Data Talk Resources
- YouCubed provides activities, videos, and research findings for data talks.7
- The New York Times provides various visualizations of real data that educators and students can discuss to foster a mathematics discourse.8
- Educators can use various visualizations featured on the Slow Reveal Graphs website to facilitate discourse about data and their implications.9
Sources
[1] https://www.youcubed.org/resource/k-8-curriculum/
[2] https://www.youcubed.org/resources/jo-teaching-visual-dot-card-number-talk/
[3] https://www.sfusdmath.org/math-talks-resources.html
[4] https://www.insidemathematics.org/classroom-videos/number-talks
[6] https://www.youcubed.org/resource/number-sense/
[7] https://www.youcubed.org/resource/data-talks/
[8] https://www.nytimes.com/column/whats-going-on-in-this-graph