Figure 6.1. Progression of Big Ideas, Transitional Kindergarten Through Grade Two (Figure 6.3 in the 2023 CA Mathematics Framework)
| Content Connections | Big Ideas: Transitional Kindergarten | Big Ideas: Kindergarten | Big Ideas: Grade One | Big Ideas: Grade Two |
|---|---|---|---|---|
| Reasoning with Data | Measure and order | Sort and describe data | Make sense of data | Represent data |
| Reasoning with Data | Look for patterns | n/a | Measuring with objects | Measure and compare objects |
| Exploring Changing Quantities | Measure and order | How many? | Measuring with objects | Dollars and cents |
| Exploring Changing Quantities | Count to 10 | Bigger or equal | Clocks and time | Problem solving with measures |
| Exploring Changing Quantities | n/a | n/a | Equal expressions | n/a |
| Exploring Changing Quantities | n/a | n/a | Reasoning about equality | n/a |
| Taking Wholes Apart, Putting Parts Together | Create patterns | Being flexible within 10 | Tens and ones | Skip counting to 100 |
| Taking Wholes Apart, Putting Parts Together | Look for Patterns | Place and position of numbers | n/a | Number strategies |
| Taking Wholes Apart, Putting Parts Together | See and use shapes | Model with numbers | n/a | n/a |
| Discovering Shape and Space | See and use shapes | Shapes in the world | Equal parts inside shapes | Seeing fractions in shapes |
| Discovering Shape and Space | Make and measure shapes | Making shapes from parts | n/a | Squares in an array |
| Discovering Shape and Space | Shapes in space | n/a | n/a | n/a |
In the primary grades, students begin the important work of making sense of the number system, implementing SMP.2 to “Reason abstractly and quantitatively.” Students engage deeply with CC3 (CC3, Taking Wholes Apart and Putting Parts Together), as they learn to count and compare, decompose, and recompose numbers. Building on a TK understanding that putting two groups of objects together will make a bigger group (addition), kindergarteners learn to take groups of objects apart, forming smaller groups (subtraction). Students develop meanings for addition and subtraction as they encounter problem situations in TK–2. They expand their ability to represent problems, and they use increasingly sophisticated methods to find answers.
Big Ideas of number in TK–2 include the following (Boaler, Munson, & Williams, 2020):
- Organize and count with numbers
- Compare and order numbers on a line
- Operate with numbers flexibly
The big ideas of data in these early grades include the following:
- Data for understanding: What questions can be asked? What data is needed to answer it?
- Defining data: What is data? How was the data collected?
- Representing and interpreting data: What does data look like, and what does it mean?
In grades TK–2, students learn to distinguish between categorical (non-numerical) data and measurement or quantitative data. For instance, consider a set of colored blocks in the classroom. “Color” is a categorical variable that students could observe about each block. “This block is 15 centimeters long” is a measurement data point. The standards develop categorical data in grades K–3 and measurement data beginning in grade two.
Figure 6.2. Examples of Categorical and Quantitative Data
| Types of Data | Examples |
|---|---|
| Quantitative (or Measurement) data |
|
| Quantitative (or Measurement) data |
|
Shape and space are important parts of TK–2 since students are learning to make sense of the world around them, while noticing patterns, common shapes, along with their attributes. As students develop their understanding of plane figures, while noting sides, angles, and similarities and differences across plane figures, students move on to see that plane shapes make up the faces of solids. The importance of shape and space is heightened by the mathematical thinking that goes into defining and describing the world, as well as students building their academic vocabulary and ability to communicate their reasoning. Patterning is another critical area. Recognizing a pattern well enough to continue it or fill in missing pieces and then generalizing the pattern is crucial to mathematical development. It is important that students focus on the unit that repeats and makes the pattern since the idea of a “unit” is used throughout TK–12 mathematics.
Students can be surrounded with a wealth of two-dimensional (2-D) and 3-D manipulatives where they can build and create, noting the composition and decomposition of the shapes that make up the world. In an online environment, teachers can ask students to look through their area for 2-D and 3-D objects. Pebbles, stones, boxes, or other items can be stacked. Describing and noticing the shapes that make up other complex shapes is an important creative way to make sense of the space around them. Students can upload pictures of what they create and describe and classify their creations. In a purely online environment, students can use the geometry in Desmos to create 2-D and 3-D shapes. Creating 2-D images of 3-D shapes is a wonderful learning experience. TapTap Blocks is a free and fun space for building in 3-D on an Apple device. Tinkercad is another option for 3-D building.
The following interview highlights an educator who is using digital tools to help students build foundational concepts introduced in this grade span.
Voices from the Field
Lisa Nowakowski | King City Union School District | King City, CA
“Helping teachers find engaging and effective ways to teach mathematics via distance learning comes down to finding the right tools for the job,” says technology coach Lisa Nowakowski. Just as she teaches students to build on existing knowledge and skills when solving math problems, Nowakowski tailors her educational technology recommendations to teachers based on what they and their learners already know. She looks for tools that are easy to adapt to existing practices and readily enhance learning experiences without putting additional strain on teachers and students.
In her 26 years as an educator, Nowakowski has taught everything from kindergarten through fifth grade and is currently a technology coach for the King City Union School District in California’s central coast. She shares how she collaborates with teachers to integrate technology efficiently and dynamically to teach math to elementary students.
How have you been helping teachers and students thrive through distance learning?
Several years ago, I developed MathReps for my fifth graders. The idea was to help them practice and retain math skills because, by the end of the year, they would get rusty and forget concepts they learned at the beginning of the year. As I developed the lessons, which were making a huge difference with my own students, I posted them online, free for other teachers to use. When we went to distance learning, teachers have shared with me that they’ve been adapting these resources using digital tools. For example, Flipgrid (video-based discussion software) and Jamboards (collaborative digital whiteboards) were used to allow students to not only show their work, but also explain and talk to each other about how they got their answers.
In what ways do you employ digital tools to enhance what may be done in a traditional classroom setting?
I just ran this activity in a class of first graders with a puzzle that had pictures of four dogs. They learned to articulate the similarities and differences they saw—this one had spots, or this one was tiny or extra-long, or all of these other dogs are the same height. The activity is adaptable, too, because I then leveled it up for a class of second graders, where they had to verbalize their rationale and also type it out on Nearpod’s [a formative assessment platform] collaborative board. We talked it out so that, just like in a traditional classroom, if you weren’t sure what to do, you could hear other examples and see how other students were thinking about it virtually.
What we’re trying to do is still have those group conversations, which are so powerful and needed—and not just for developing math sense. My district has a high number of students who are ELs; it’s really important for them to be talking about these things just to hear the different vocabulary and to practice speaking and listening. Having activities and dedicated space to be able to talk things out is simple, but so powerful.
What’s the best way to balance synchronous and asynchronous learning experiences for students?
What we do is try and make asynchronous assignments engaging and fun—something that isn’t boring and that they may already have familiarity and success with. For the synchronous work, we schedule in the higher level, harder concepts that they need more guidance through. Once they get more proficient at those skills, then those get moved to asynchronous assignments, and so on. The teachers in our district are really just trying to balance the learning experience to make it as engaging and interesting as possible.
How are you using technology to help students learn foundational math concepts?
If you’re having students solve 36 + 45, for example, and asking them to think about different ways to break these numbers apart, you can use Jamboard (collaborative digital whiteboards), and they can write out their reasoning, like 30 + 40 and then 6 + 5 on virtual sticky notes, or if they already know Google Slides, you can have them each make their own presentation or make videos on Flipgrid (video-based discussion software) to explain their logic. Just like when solving math problems, there are multiple paths to the right answer—it’s really whatever tool works best for you and your students.
As the technology coach, people often ask me what the best tool is, and I always tell them it’s really about what they are trying to do and how. We’ll talk about the tools they’re already using and then build from there. I don’t rely on one-size-fits-all recommendations for everyone because, just like we have to be flexible with numbers, we have to be flexible with the tools we use. It’s about finding the right tool for the job.
Transitional Kindergarten
The work of learning to count typically begins in the preschool years. The California Preschool Learning Foundations, Volume 1 includes foundations in mathematics that cover five strands: Number Sense, Algebra and Functions (Classification and Patterning), Measurement, Geometry, and Mathematical Reasoning. These foundations in mathematics support the developmental progression of students from preschool through TK.1
In TK, students are working out what numbers mean and how numbers connect to fingers, objects, movement, and each other. Students learn to count objects meaningfully by touching objects one-by-one as they name the quantities, recognizing that the total quantity is identified by the name of the last object counted (cardinality). As students compare numbers, they will later be able to locate them on a line. Number lines are really helpful for students’ learning and have even been found to eliminate differences in numerical reasoning between middle income and lower income students in preschool (Ramani & Siegler, 2008).
Figure 6.3. A Number Line

In TK, kindergarten, and first grade, a more accessible model is a number path. Whereas a number line shows numbers in terms of measurement, a number path is a counting model, which shows numbers as rectangles.
Figure 6.4. A Number Path

When young students count on a number line, they can miss the numbers and land on the spaces, whereas a number path allows students to count the rectangles.2
In TK, students start to compare data and numbers using objects and learn relational vocabulary, such as more, fewer, less, same as, greater than, less than, and more than. Dot card number talks (see figure 6.4) are an ideal activity for students to learn to subitize, identifying a small group, in this case dots, without counting. Activities can be designed in ways that provide students with a variety of structures to practice, engage with, and eventually master the vocabulary. In TK, students learn to distinguish between categorical (non-numerical) data, such as color, and measurement or quantitative data, such as the height of a plant.
Young children love to build and create. Students can be encouraged to develop creative scenes using 2-D shapes, as well as create linear patterns and arrays of shapes, including composing simple shapes to form complex ones. An important concept for students to learn is that shapes can transform in space and maintain their congruence. For example, a triangle can spin and flip, but it is still the same triangle just oriented in space differently. Allow students time and space to play with shapes. They can be encouraged to describe a shape’s position in space compared to other shapes and start to use language that describes similarities and differences in shapes, as well as magnitude, direction, and distance.
Patterns are a natural beginning to mathematical thinking for young children. This is a time where seeing patterns supports a young learner in making sense of their world. Students can be encouraged to notice patterns in everything they experience, in school and at home, and can be encouraged to describe and communicate the attributes they see and the ways they see the patterns. Students can be asked to describe what would come next, solidifying that they have recognized a pattern. The physical act of building or continuing the pattern is the next important piece in their growth, culminating in their ability to communicate a generalized statement about the pattern. Students who are ELs are encouraged to use their developing English and native language assets and draw on their prior knowledge. Teachers can provide purposefully planned and “just-in-time” scaffolds and supports to engage EL students in sustained mathematical oral discourse in multiple contexts to build academic vocabulary and knowledge.
TK instruction can create rich, effective discussion where students use developing skills to clarify, inform, question, and eventually employ these conversational behaviors without direct prompting. Such instruction supports all students, including EL students, and ensures all learners develop both mathematics content and language. TK students can compare collections of small objects as they play fair share games, deciding who has more; by lining up the two collections side by side, children can make sense of the question and practice the relevant vocabulary. As the students develop understanding in recognizing numerals, they can play games with cards. The use of fingers is particularly important for students of this age, as they can represent early ideas of a number line.
Critical Areas of Instructional Focus for Transitional Kindergarten
Figure 6.5. Transitional Kindergarten Big Ideas (Figure 6.8 in the 2023 CA Mathematics Framework)
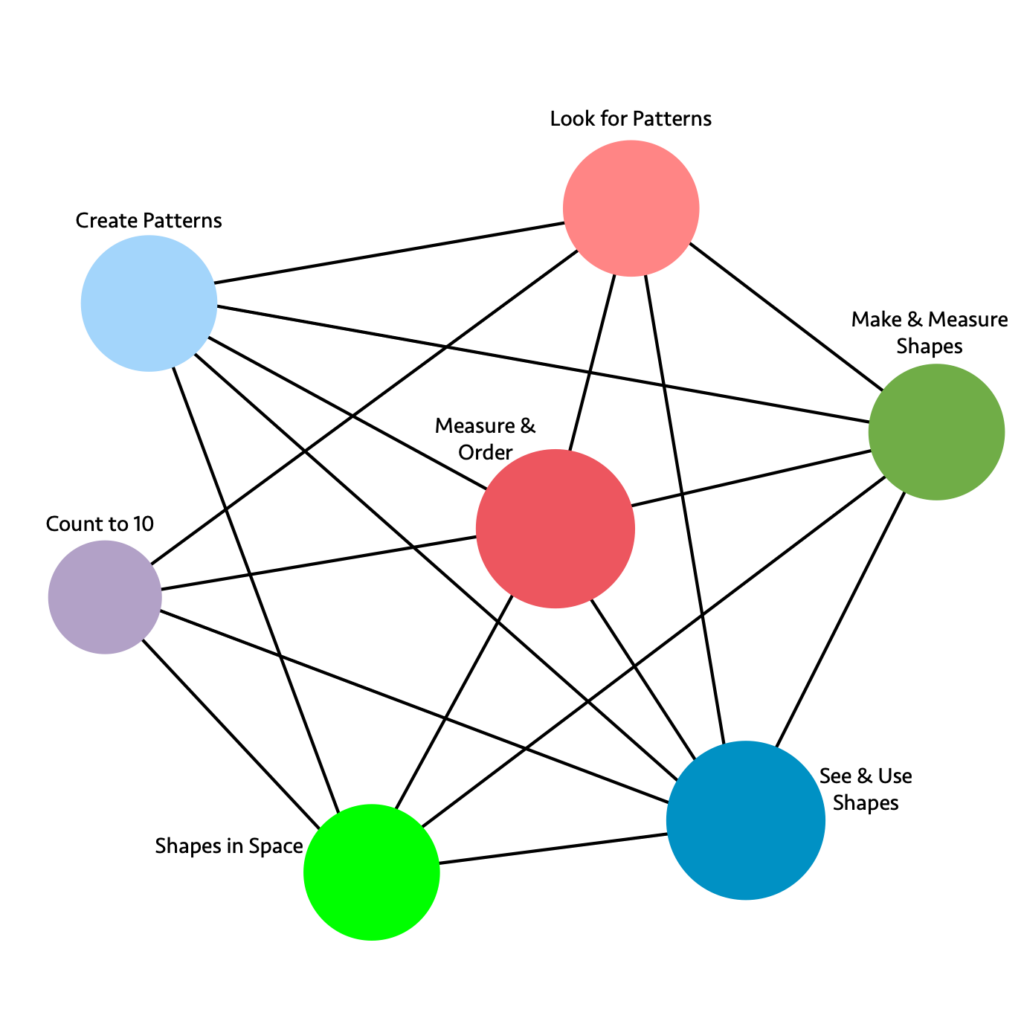
Long description: The graphic illustrates the connections and relationships of some transitional kindergarten mathematics concepts.
Direct connections include:
- Look for Patterns directly connects to: Create Patterns, Count to 10, Measure and Order, See and Use Shapes, Make and Measure Shapes
- Make and Measure Shapes directly connects to: Look for Patterns, Create Patterns, Measure and Order, Shapes in Space, See and Use Shapes
- See and Use Shapes directly connects to: Make and Measure Shapes, Look for Patterns, Measure and Order, Create Patterns, Count to 10, Shapes in Space
- Shapes in Space directly connects to: See and Use Shapes, Make and Measure Shapes, Measure and Order, Create Patterns, Count to 10
- Count to 10 directly connects to: Shapes in Space, See and Use Shapes, Measure and Order, Look for Patterns
- Create Patterns directly connects to: Look for Patterns, Make and Measure Shapes, See and Use Shapes, Measure and Order, Shapes in Space
- Measure and Order directly connects to: Look for Patterns, Make and Measure Shapes, See and Use Shapes, Shapes in Space, Count to 10, Create Patterns
Figure 6.5a. Transitional Kindergarten Big Ideas, Content Connections, and Content Standards (Figure 6.9 in the 2023 CA Mathematics Framework)
| Big Ideas | Content Connections | Transitional Kindergarten Content Standards |
|---|---|---|
| Measure and Order | Reasoning with Data and Exploring Changing Quantities |
AF1.1, M1.1, M1.2, M1.3, NS2.1, NS2.3, NS1.3, G 1.1, G2.1 NS1.4, NS1.5, MR1.1, NS1.1, NS1.2: Compare, order, count, and measure objects in the world. Learn to work out the number of objects by grouping and recognize up to 4 objects without counting. |
| Look for Patterns | Reasoning with Data and Taking Wholes Apart, Putting Parts Together |
AF2.1, AF2.2: NS1.3, NS1.4, NS1.5, NS2.1, NS2.3, G1.1, M1.2: Recognize and duplicate patterns – understand the core unit in a repeating pattern. Notice size differences in similar shapes. |
| Count to 10 | Exploring Changing Quantities | NS1.4, MR1.1, AF1.1, NS2.2: Count up to 10 using one to one correspondence. Know that adding or taking away 1 makes the group larger or smaller by 1. |
| Create Patterns | Taking Wholes Apart, Putting Parts Together | AF2.2, AF2.1, M1.2, G1.1, G1.2, G2.1: Create patterns – using claps, signs, blocks, shapes. Use similar shapes to make a pattern and identify size differences in the patterns. |
| See and Use Shapes | Taking Wholes Apart, Putting Parts Together and Discovering Shape and Space |
G1.1, G1.2, NS2.3, NS1.4, MR1.1: Combine different shapes to create a picture or design and recognize individual shapes, identifying how many shapes there are. |
| Make and Measure Shapes | Discovering Shape and Space | G1.1, M1.1, M1.2, NS1.4: Create and measure different shapes. Identify size differences in similar shapes. |
| Shapes in Space | Discovering Shape and Space | G2.1, M1.1, MR1.1: Visualize shapes and solids (2-D and 3-D) in different positions, including nesting shapes, and learn to describe direction, distance, and location in space. |
Figure 6.5a includes Preschool Foundations in mathematics for students at around 60 months of age. The related kindergarten standards for TK are identified in the next section.
Kindergarten
In kindergarten, instructional time focuses on two critical areas: (1) representing and comparing whole numbers, initially with sets of objects, and (2) describing shapes and space. In kindergarten, as in TK, students are working out what numbers mean––how numbers connect to fingers, objects, movement, and each other. As students compare numbers, they will later be able to locate them on a line. Number lines are really helpful for students’ learning and have even been found to eliminate differences in numerical reasoning between middle income and lower income students in preschool (Ramani & Siegler, 2008).
Figure 6.6. A Number Line

In kindergarten and first grade, a more accessible model is a number path. Whereas a number line shows numbers in terms of measurement, a number path is a counting model, which shows numbers as rectangles.3
Figure 6.7. A Number Path

When young students count on a number line, they can miss the numbers and land on the spaces, whereas a number path allows students to count the rectangles.
Number talks are a particularly effective way for students to learn to compose and decompose numbers. In kindergarten, children become familiar with numbers from 1–20, and they count quantities up through 10 accurately when presented in various configurations. The use of fingers is particularly important for students of this age, as they can represent early ideas of a number line. Dot card number talks (see figure 6.7) are an ideal activity for students to learn to subitize, identifying a group of dots without counting. As students begin seeing groups of dots as a quantity without the need for counting, they are able to partition larger groups of dots in known subitized groups, forming an important part of their number flexibility journey. Of particular importance is how numbers (and the objects they represent) and shapes can be put together and taken apart to create something new, but related. These are important ideas for the area: Taking wholes apart, putting parts together. These are powerful early steps in encouraging students to look for and name mathematical connections. As students engage in number sense explorations, activities, and games, they develop the capacity to reason abstractly and quantitatively (SMP.2) and model mathematical situations symbolically and with words (SMP.4).
As kindergarten students consider “Which has more?” questions, they can work with data, asking questions, such as “I wonder which shape has more sides?” and “Which kind of block is heaviest?” In addition to questions that can be answered with a single value, students can start to pose statistical investigative questions that involve multiple variables, such as “I wonder if plants grow more with additional sunlight?” or “I wonder if age affects which color people like?” Across the learning of different mathematical areas, students can be encouraged to use words and drawings to make convincing arguments to justify work. Students who are ELs are encouraged to use their developing English and native language assets and draw on their prior knowledge. Teachers can provide purposefully planned and “just-in-time” scaffolds and supports to engage EL students in sustained mathematical oral discourse in multiple contexts to build academic vocabulary and knowledge.
Students in kindergarten continue their exploration of geometric shapes by noticing similarities and differences in the shapes. Students can use the geometry in Desmos to create 2-D and 3-D shapes. Creating 2-D images of 3-D shapes is a wonderful learning experience. TapTap Blocks is a free space for building in 3-D on an Apple device. Tinkercad is another good option for 3-D building. When students are initially allowed to use their own words and engage with others, their use of academic vocabulary increases as they learn to describe these similarities and differences. Shapes can be beautifully connected with categorical data as students organize shapes that are squares, triangles, and circles, as well as numerical data as they note which shapes have three sides or four angles, for example. Sorting activities support students’ growth in mathematics, especially when students are given sets of objects where they, themselves, determine the categorical or numerical variables and communicate their reasoning to others. As students sort and label the attributes, they are also pattern seeking. 3-D shapes, solids, can be introduced, and students again can be asked to sort sets of 2-D and 3-D objects. Through this activity, they will notice that the 3-D shape faces are similar to the 2-D shapes, as composing and decomposing shapes allows students opportunities to see shapes within shapes. As students progress to seeing the relevance of 2-D shapes within 3-D shapes, they can be encouraged to combine different 3-D shapes, composing more complex shapes. It is important to include composing and decomposing shapes so students can see shapes within shapes.
Patterns are an important part of all grade levels, especially in the primary grades, as pattern seeking is the essence of mathematics (Devlin, 1996). Minds seek patterns to make sense of the world. As students work with AB and ABA patterns and more, they are forming an important knowledge set. Attention can be paid to the repetitive unit. While it is important to fill in the gaps in a pattern or predict what comes next, careful attention can be paid to the set of items that form the base unit of the pattern. For example, a pattern where students are asked to fill in the blank (e.g., square, triangle, square, ?, square, triangle) should include a conversation about the unit that repeats. Students note that “square, triangle” is the unit that repeats itself. Pattern exploration can extend to students’ homes and lives as they learn to see and explore patterns all around them.
Critical Areas of Instructional Focus for Kindergarten
Figure 6.8. Kindergarten Big Ideas (Figure 6.10 in the 2023 CA Mathematics Framework)

Long description: The graphic illustrates the connections and relationships of some kindergarten mathematics concepts.
Direct connections include:
- How Many directly connects to: Being flexible within 10, Shapes in the World, Sort and Describe Data, Bigger or Equal, Place and Position of Numbers
- Model with Numbers directly connects to: Being flexible within 10, Sort and Describe Data, Place and Position of Numbers
- Being Flexible within 10 directly connects to: Model with Numbers, How Many, Making Shapes from Parts, Shapes in the World
- Shapes in the World directly connects to: Being flexible within 10, How Many, Sort and Describe Data, Bigger or Equal, Making Shapes from Parts
- Making Shapes from Parts directly connects to: Shapes in the World, Being flexible within 10, Sort and Describe Data, Bigger or Equal
- Bigger or Equal directly connects to: Making Shapes from Parts, Shapes in the World, Sort and Describe Data, How Many
- Place and Position of Numbers directly connects to: How Many, Model with Numbers, Sort and Describe Data
- Sort and Describe Data directly connects to: How Many, Model with Numbers, Shapes in the World, Making Shapes from Parts, Bigger or Equal, Place and Position of Numbers
Figure 6.8a. Kindergarten Big Ideas, Content Connections, and Content Standards (Figure 6.11 in the 2023 CA Mathematics Framework)
| Big Ideas | Content Connections | Kindergarten Content Standards |
|---|---|---|
| Sort and Describe Data | Reasoning with Data | MD.1, MD.2, MD.3, CC.4, CC.5, G.4: Sort, count, classify, compare, and describe objects using numbers for length, weight, or other attributes |
| How Many? | Exploring Changing Quantities | CC.1, CC.2, CC.3, CC.4, CC.5, CC.6, CC.7, MD.3: Know number names and the count sequence to determine how many are in a group of objects arranged in a line, array, or circle. Fingers are important representations of numbers. Use words and drawings to make convincing arguments to justify work. |
| Bigger or Equal? | Exploring Changing Quantities | CC.4, CC.5, CC.6, MD.2, G.4: Identify a number of objects as greater than, less than, or equal to the number of objects in another group. Justify or prove your findings with number sentences and other representations. |
| Being Flexible within 10 | Taking Wholes Apart, Putting Parts Together | OA.1, OA.2, OA.3, OA.4, OA.5, CC.6, G.6: Make 10, add and subtract within 10, compose and decompose within 10 (find 2 numbers to make 10). Fingers are important. |
| Place and Position of Numbers | Taking Wholes Apart, Putting Parts Together | CC.3, CC.5, NBT.1: Get to know numbers between 11 and 19 by name and expanded notation to become familiar with place value, for example: 14 = 10 + 4. |
| Model with Numbers | Taking Wholes Apart, Putting Parts Together | OA.1, OA.2, OA.5, NBT.1, MD.2: Add, subtract, and model abstract problems with fingers, other manipulatives, sounds, movement, words, and models. |
| Shapes in the World | Discovering Shape and Space | G.1, G.2, G.3, G.4, G.5, G.6, MD.1, MD.2, MD.3: Describe the physical world using shapes. Create 2-D and 3-D shapes, and analyze and compare them. |
| Making Shapes from Parts | Discovering Shape and Space | MD.1, MD.2, G.4, G.5, G.6: Compose larger shapes by combining known shapes. Explore similarities and differences of shapes using numbers and measurements. |
Grade One
Organizing and seeing equivalence are ideas that pervade first grade. Students develop ways to organize to help them with counting and comparing and ultimately understanding the place value system. Grade one students will compare two, two-digit numbers based on the meanings of the tens and the ones digits, which is an important concept (SMP.1, 2; 1.NBT.3). To gain this understanding, students have worked extensively creating tens from collections of ones and have internalized the idea of a “ten.” Younger learners typically count by ones, and may show little or no grouping or organization of objects as they count. As they acquire greater confidence and understanding, children can progress to counting some of the objects in groups of 5 or 10. Teachers may support student learning by providing interesting, varied, and frequent counting opportunities using games, group activities, and a variety of tools, along with focused mathematical discourse. Students who are ELs are encouraged to use their developing English and native language assets and draw on their prior knowledge. Teachers can provide purposefully planned and “just-in-time” scaffolds and supports to engage EL students in sustained mathematical oral discourse in multiple contexts to build academic vocabulary and knowledge.
Equivalence means learning to assess what makes things different and the same. For instance, 4 + 1 and 5 are equivalent, even though they look different, and students may develop a dozen strategies for adding 4 and 1 to arrive at 5. Those strategies are different but related and equivalent in the result they produce. Grappling with equivalence and organization is important work in first grade.
Posing questions as students are engaged in the activities can help a child see relationships and further develop place value concepts. Some questions might include the following:
- What do you notice?
- What do you wonder?
- What will happen if we count these by ones?
- What if we counted them in groups of ten?
- How can we be sure there really are 43 here?
- I see you counted by groups of 10 and ones. What if you counted them all by ones? How many would we get?
Teachers can have students assemble bundles of 10 objects (popsicle sticks or straws, for example), or snap together linking cubes to make tens as a means of developing the concept and noting how the quantities are related. Note that while students in first grade do begin to add two-digit numbers, they do so using strategies as distinguished from formal algorithms. The CA CCSSM intentionally place the introduction of a standard algorithm for addition and subtraction in fourth grade (4.NBT.4). Examples of useful manipulatives at this age include 10-frames, Rekenreks, comparison bars, Cuisenaire rods, and useful visuals include hundreds charts, 0–99 charts, and number paths. Fingers continue to be important. NRICH provides online Cuisenaire Rods, and other moveable shapes.4
In first grade, students can conduct data investigations, generating questions to study, using measurements of length and time, along with continued work categorizing and counting objects, and categorizing geometric objects by attributes. When conducting data investigations, it is important to avoid questions about students’ physical attributes or possessions, even those that seem innocuous, such as height or arm length. Instead, some good questions to wonder about might be “I wonder what time it will be when the next person walks into the classroom?” or “I wonder which book in the classroom is the most read?,” comparing events or objects rather than personal characteristics. Guidance cards can provide additional support to help EL students engage in structured explorations of the Big Ideas (What you can do) and communicate (What you can say) with peers.
Students extend their work from kindergarten, focusing on 2-D shapes in a flat surface, to considering ways these shapes are the faces of 3-D shapes that make up the world. Students can work qualitatively and quantitatively with shapes, using their language to describe the similarities and differences, and counting and joining numbers to describe the shapes. For example, a student might notice a cube has four corners when looking directly at the square that forms one of its six faces. Students can count the corners, or vertices, and notice that a cube has eight vertices and six square faces. A student may then notice that a prism has the same number of faces and vertices, but four of the faces are rectangles and the other two faces are squares. Including the circle as an additional shape brings in discussion about cylinders and cones. The circle is an important shape to discuss, as all circles are similar. Students also see the circle as an item that can be constructed from sectors or pieces. Constructing circles, and playing with pieces that combine to make a circle, begins an important journey towards fractions and telling the time on an analog clock.
Critical Areas of Instructional Focus for Grade One
Figure 6.9. Grade One Big Ideas (Figure 6.12 in the 2023 CA Mathematics Framework)

Long description: The graphic illustrates the connections and relationships of some first-grade mathematics concepts.
Direct connections include:
- Clocks and Time directly connects to: Equal Parts Inside Shapes, Reasoning About Equality, Make Sense of Data, Tens and Ones
- Equal Expressions directly connects to: Reasoning About Equality, Make Sense of Data, Tens and Ones, Measuring with Objects
- Reasoning About Equality directly connects to: Equal Expressions, Clocks and Time, Make Sense of Data, Tens and Ones
- Tens and Ones directly connects to: Reasoning About Equality, Make Sense of Data, Equal Expressions, Clocks and Time
- Measuring with Objects directly connects to: Equal Expressions, Make Sense of Data
- Equal Parts Inside Shapes directly connects to: Clocks and Time, Make Sense of Data
- Make Sense of Data directly connects to: Reasoning About Equality, Tens and Ones, Measuring with Objects, Clocks and Time, Equal Expressions, Equal Parts Inside Shapes
Figure 6.9a. Grade One Big Ideas, Content Connections, and Content Standards (Figure 6.13 in the 2023 CA Mathematics Framework)
| Big Ideas | Content Connections | Grade One Content Standards |
|---|---|---|
| Make Sense of Data | Reasoning with Data | MD.2, MD.4, MD.3, MD.1, NBT.1, OA.1, OA.2, OA.3: Organize, order, represent, and interpret data with two or more categories; ask and answer questions about the total number of data points, how many are in each category, and how many more or less are in one category than in another. |
| Measuring with Objects | Reasoning with Data and Exploring Changing Quantities |
MD.1 MD.2, OA.5: Express the length of an object by units of measurement e.g., the stapler is 5 red Cuisenaire rods long, the red rod representing the unit of measure. Understand that the measurement length of an object is the number of units used to measure. |
| Clocks and Time | Exploring Changing Quantities | MD.3, NBT.2, G.3: Read and express time on digital and analog clocks using units of an hour or half hour. |
| Equal Expressions | Exploring Changing Quantities | OA.6, OA.7, OA.2, OA.1, OA.8, OA.5, OA.4, OA.3, NBT.4: Understand addition and subtraction, using various models, such as connected cubes. Compose and decompose numbers to make equal expressions, knowing that equals means that both sides of an expression are the same (and it is not simply the result of an operation). |
| Reasoning About Equality | Exploring Changing Quantities | OA.3, OA.6, OA.7, NBT.2, NBT.3, NBT.4: Justify reasoning about equal amounts, using flexible number strategies (e.g., students use compensation strategies to justify number sentences, such as 23 – 7 = 24 – 8). |
| Tens and Ones | Taking Wholes Apart, Putting Parts Together | NBT.4, NBT.3, NBT.1, NBT.2, NBT.6, NBT.5: Think of whole numbers between 10 and 100 in terms of tens and ones. Through activities that build number sense, students understand the order of the counting numbers and their relative magnitudes. |
| Equal Parts Inside Shapes | Discovering Shape and Space | G.3, G.2, G.1, MD.3: Compose 2-D shapes on a plane as well as in 3-D space to create cubes, prisms, cylinders, and cones. Shapes can also be decomposed into equal shares, as in a circle broken into halves and quarters defines a clock face. |
Grade Two
In second grade students start to think deeply about familiar benchmark or “friendly” numbers, so they can use them to compose, decompose, and compare numbers. In second grade, students extend their understanding of place value and number comparison to include three-digit numbers. To compare two three-digit numbers, second graders can take the number apart by place value and compare the number of hundreds, tens, and ones, or they may use counting strategies. Thinking with numbers, such as ones, tens, and hundreds, and negotiating how to use them as groups and as positions on the number line to solve problems, is central to this grade. Students continually anchor their thinking about number to all the real-world places where numbers are used to describe and wonder, including estimating lengths and quantities and thinking with data. Note that while students in second grade do begin to subtract numbers, they do so using strategies as distinguished from formal algorithms.
In second grade, students can conduct data investigations and interpret data visuals through data talks. Students continue to use measurement of length and time as contexts in generating questions, along with continued work categorizing and counting objects and categorizing geometric objects by attributes. In second grade, students also start to use the context of money. When conducting data investigations, it is important to avoid questions about students’ physical attributes or possessions, even those that seem innocuous, such as hair color or shoe type. Instead, some good questions to wonder about might be “I wonder what time it will be when the next person walks into the classroom?” or “I wonder which book in the classroom is the most read?,” comparing events or objects rather than personal characteristics. Students who are ELs are encouraged to use their developing English and native language assets and draw on their prior knowledge. Teachers can examine text and tasks for key language forms and structures, and general as well as discipline-specific, high-utility academic vocabulary words linked to the Big Ideas and connections. Teachers can provide purposefully planned and “just-in-time” scaffolds and supports to engage EL students in sustained mathematical discourse in multiple contexts to build academic language and knowledge.
Grade two begins more formal vocabulary use and the connections between numbers and shapes. Students continue to work with 2-D and 3-D shapes, composing and decomposing within a plane or space, as they refine their understanding of figures that have area and those that have volume. Students begin to partition shapes into equal units, known as unit fractions. This is especially important in circles and will be the base understanding of navigating time using an analog clock.
Students learn in second grade that they can partition rectangles into arrays of equal squares and quantify the lengths of sides by using a unit to measure. For example, a student may use a light green Cuisenaire rod to approximate the length of a stapler or a stack of 5 Unifix cubes to measure the same length. This can lead to discussion of the importance of a base unit as the length that is used to quantify. Equal partitions are also of utmost importance, as students begin to understand the idea of a fraction.
Critical Areas of Instructional Focus for Grade Two
Figure 6.10. Grade Two Big Ideas (Figure 6.14 in the 2023 CA Mathematics Framework)

Long description: The graphic illustrates the connections and relationships of some second-grade mathematics concepts.
Direct connections include:
- Dollars and Cents directly connects to: Problems Solving with Measure, Skip Counting to 100, Number Strategies, Represent Data
- Problems Solving with Measure directly connects to: Skip Counting to 100, Number Strategies, Represent Data, Measure and Compare Objects, Dollars and Cents
- Skip Counting to 100 directly connects to: Number Strategies, Seeing Fractions in Shapes, Squares in an Array, Represent Data, Dollars and Cents, Problems Solving with Measure
- Number Strategies directly connects to: Skip Counting to 100, Problems Solving with Measure, Dollars and Cents, Represent Data
- Seeing Fractions in Shapes directly connects to: Skip Counting to 100, Represent Data, Squares in an Array
- Squares in an Array directly connects to: Seeing Fractions in Shapes, Skip Counting to 100, Represent Data, Measure and Compare Objects
- Measure and Compare Objects directly connects to: Squares in an Array, Represent Data, Problems Solving with Measure
- Represent Data directly connects to: Measure and Compare Objects, Dollars and Cents, Problems Solving with Measure, Skip Counting to 100, Number Strategies, Seeing Fractions in Shapes, Squares in an Array
Figure 6.10a. Grade Two Big Ideas, Content Connections, and Content Standards (Figure 6.15 in the 2023 CA Mathematics Framework)
| Big Ideas | Content Connections | Grade Two Content Standards |
|---|---|---|
| Measure and Compare Objects | Reasoning with Data | MD.1, MD.2, MD.3, MD.4, MD.6, MD.9: Determine the length of objects using standard units of measures, and use appropriate tools to classify objects, interpreting and comparing linear measures on a number line. |
| Represent Data | Reasoning with Data | MD.7, MD.9, MD.10, G.2, G.3, NBT.2: Represent data by using line plots, picture graphs, and bar graphs, and interpret data in different data representations, including clock faces to the nearest 5 minutes. |
| Dollars and Cents | Exploring Changing Quantities | MD.8, MD.5, NBT.1, NBT.2, NBT.5, NBT.6, NBT.7: Understand the unit values of money and compute different values when combining dollars and cents. |
| Problem Solving with Measure | Exploring Changing Quantities and Discovering Shape and Space |
NBT.7, NBT.1, MD.1, MD.2, MD.3, MD.4, MD.5, MD.6, MD.9, OA.1: Solve problems involving length measures using addition and subtraction. |
| Skip Counting to 100 | Taking Wholes Apart, Putting Parts Together | NBT.1, NBT.3, NBT.7, OA.4, G.2: Use skip counting, counting bundles of 10, and expanded notation to understand the composition and place value of numbers up to 1,000. This includes ideas of counting in fives, tens, and multiples of hundreds, tens, and ones, as well as number relationships involving these units, including comparing. |
| Number Strategies | Taking Wholes Apart, Putting Parts Together | MD.5, NBT.5, NBT.6, NBT.7, OA.1, OA.2: Add and subtract 2-digit numbers, within 100, without using algorithms––instead encouraging different strategies and justification. Compare and contrast the different strategies using models, symbols, and drawings. |
| Seeing Fractions in Shapes | Discovering Shape and Space | G.1, G.2, G.3, MD.7: Divide circles and rectangles into equal shares and know them to be standard unit fractions. Identify and draw 2-D and 3-D shapes, recognizing faces and angles. |
| Squares in an Array | Discovering Shape and Space | OA.4, G.2, G.3, MD.6: Partition rectangles into rows and columns of unit squares to find the total number of square units in an array. |
Sources
[1] California Preschool Learning Foundations, Volume 1 (https://www.cde.ca.gov/sp/cd/re/documents/preschoollf.pdf)
[2] Tapfun number paths K–1 math (https://commoncoreconnectionusa.blogspot.com/2013/10/number-paths-fabulous-tool-for.html)
[3] Tapfun number paths K–1 math (https://commoncoreconnectionusa.blogspot.com/2013/10/number-paths-fabulous-tool-for.html)
[4] University of Cambridge NRICH Program (https://nrich.maths.org/)